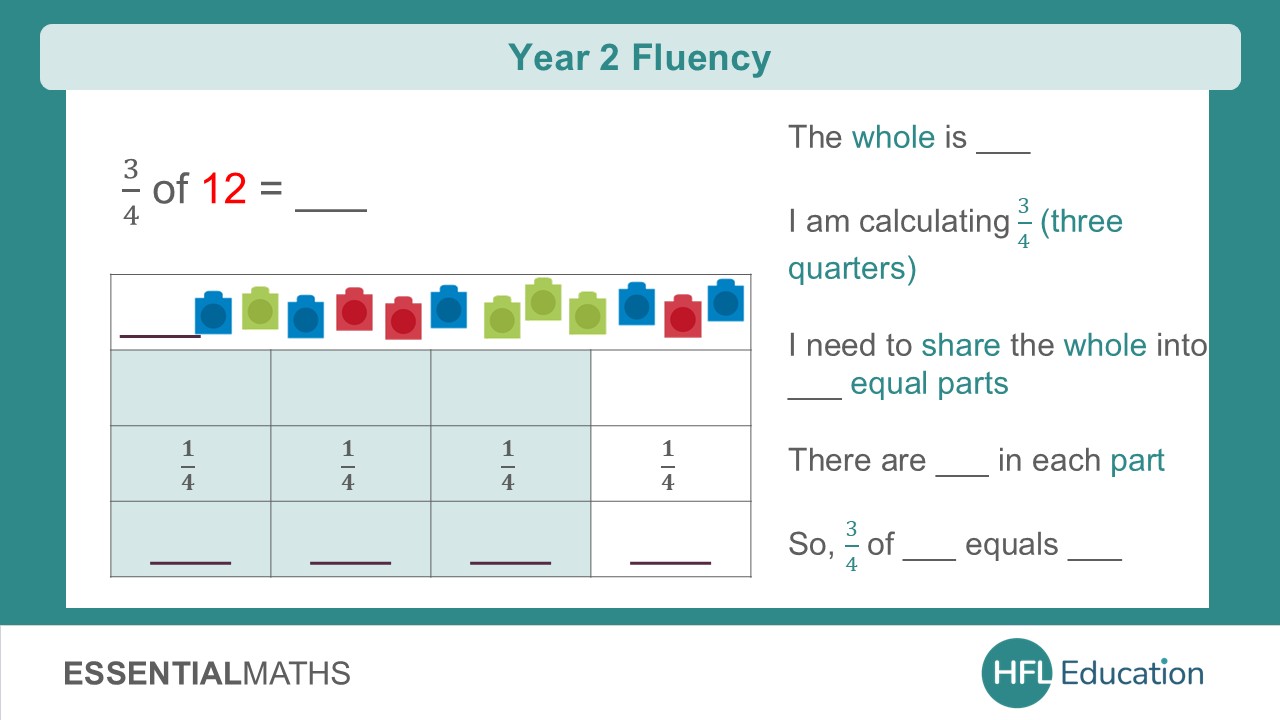
Every time I read through a new guidance document that comes out, I always ask myself what it actually means for children and teachers within the classroom. Section 4 of the Writing Framework feels particularly important because it gets right to the heart of what we do: supporting children to become confident, purposeful writers - fostering writers who can shape meaning, not just follow instructions.
What I enjoyed about this section is how clearly it positions writing as a process of thinking, not just doing. It reminds us that the quality of children’s writing is tied directly to the quality of the decisions they make - decisions about vocabulary, structure, varied sentences, tone, pace, clarity and effect. These choices aren’t made at the end - they happen all the way through.
Strong sentences, stronger writers
One thing Section 4 reinforces for me is just how important it is that we teach sentences really explicitly. Children don’t just ‘pick up’ how to write a clear, controlled sentence - they need to see it, hear it, speak it, try it, and practise it with purpose. When we break things down and actually show them how a sentence works, everything else in their writing becomes more secure. We see it often in KS2 where children try to add all the flourishes to their writing, but the basic conceptual understanding of a sentence is lost. So, they’re building on shaky foundations.
This doesn’t mean reducing writing to isolated, disconnected grammar drills. And it certainly isn’t about children tossing around random sentence types. It’s about using varied sentences purposefully, at the point where meaning is crafted, where clarity, pace, detail and intention are combined to engage our reader.
For me, explicit sentence teaching looks like modelling in the moment, thinking aloud, changing words, reshaping the structure and, most of all, explaining the why. It’s also about giving children time to rehearse sentences orally before they write them. This will help them hold the idea clearly. When we secure sentence structure, we’re giving children the core foundations to build on. Their writing becomes clearer, more cohesive and far more confident because they understand exactly what they’re trying to say and how to say it well. Activities to support children can be found within Appendix D: Examples of Sentence Structure Activities. For further support with securing the sense of a sentence, take a look at our Securing Full Stops at KS1 and Fixing Full Stops at KS2 CPD.
Vocabulary
‘Effective composition…requires…an increasingly wide knowledge of vocabulary.’ (p. 53)
When children have access to rich vocabulary and use words judiciously, everything about their writing sharpens. Their ideas land more clearly, their descriptions deepen and suddenly their sentences have more purpose and draw the reader in. But this doesn’t happen by chance. It comes from explicit vocabulary teaching. Choose the right Tier 2 words. Use child-friendly definitions. Explore them. Make connections. Rehearse them in talk. Provide meaningful opportunities for children to actually use them, not only within that one writing lesson, but across the week and across the curriculum. When we provide multiple encounters with new words, they become part of children’s long-term memory. We’re not just improving writing here; we’re expanding the boundaries of what children can think, say and create.
The importance of talk and rehearsal
One of the most practical messages is the emphasis on oral rehearsal. Before children can write something meaningful, they need time to think it through, say it, reshape it and test how it sounds.
It’s easy to forget how cognitively demanding writing is. Oral rehearsal reduces that load. It allows children to verbally practise their writing before committing it to the page. If Section 4 does anything, it certainly validates the time we spend on discussion, sentence-building and refining ideas before writing begins. This is not a warm-up, but part of essential composition work.
Reading as a foundation for writing
Reading sits underneath much of what is described. The framework is clear that children internalise patterns, rhythms and structures from the texts they encounter.
When children read widely and deeply, they absorb sentence shapes, organisational structures and vocabulary choices. All of which later become part of their writerly toolkit. When reading, draw attention to these patterns explicitly. Show children how writers achieve an effect so they can try similar moves in their own writing.
Modelling
A favourite strategy, and one I emphasise time and time again when it comes to writing, is modelling. This is the ‘I do’ before you have a go together or invite the children to try out the ideas in their own writing. Children benefit from opportunities to watch how you construct meaning, hear about the choices you make and see what the impact of your language choices can be. When in class, I used to have my own exercise book and write for and alongside the children using a visualiser. I’d model all my writerly thoughts - not presenting a completed example, but perhaps having this near me for my reference only. In your next writing lesson, try modelling your thinking, your decisions, your edits and your hesitations.
Children need to hear:
- “This word isn’t quite right - let me change it.”
- “I’m putting this sentence here because…”
- “Oh, I forgot to add…”
- “This paragraph is losing its flow and my reader might get bored – let me restructure it.”
When we model authentically, we reveal the processes behind composition rather than the polished product
Writing isn’t linear – the writing process
The framework puts forward a writing process, acknowledging the significance of each of the different phases. It is important that children know that writers go through a process from generating ideas and planning, to drafting, editing and improving their writing, ready to share with its intended audience. Understanding these steps helps children to refine their writing, to help it be the best it can be, and to achieve its intended purpose. Many authors openly share their process, and these resources can be great to show children, to help them feel part of the wider community of writers. David Almond has a fantastic page on his website, dedicated to his own creative methods.
Teaching writing as a process - rather than a one-off event – can significantly improve outcomes. It can also make the task less daunting. When children are explicitly taught strategies for planning, revising and editing, and given opportunities to make choices about their writing, they develop both skill and independence. Embedding these practices within the classroom nurtures writers who see writing as a craft: purposeful, iterative and deeply connected to audience and meaning. Each unit in our ESSENTIALWRITING curriculum ensures that children have the opportunity to go through this process, helping them to understand what it means to be a writer.
It's pleasing to see that the framework acknowledges that the writing process is recursive - a point that feels incredibly freeing. Writers and children do not plan, draft, proofread, edit and share in neat stages. They loop back. They re-read. They change their minds. They share their ideas with a friend. They refine their writing.
Our teaching can reflect this by building in:
- pit stops
- mid-draft reflections
- return-to-purpose checks
- opportunities to revise and reshape ideas.
When children see writing as a flexible process rather than a rigid sequence, they become more confident and more willing to adapt their work for clarity and meaning.
Purpose and audience as the anchor
‘For successful writing, it is important to establish a clear purpose from the beginning. Pupils should be guided to articulate their ideas and consider their audience.’ (The writing framework, p. 65)
Children should write with a clear sense of who they are writing for and why. This shapes vocabulary, structure, tone and content. When purpose and audience are made explicit from the start, writing becomes more coherent and more intentional. Children see writing not as filling space or ticking boxes, but as communicating something meaningful.
Our ESSENTIALWRITING curriculum places audience and purpose at the heart of the writing curriculum, ensuring every child understands why they are writing and who they are writing for. By making these elements explicit, the framework helps children craft meaningful texts rather than simply following instructions or tick lists which can lead to formulaic writing and a lack of motivation. A focus on audience and purpose builds confidence and competence, while fostering motivation through authentic writing experiences. As a result, pupils develop the skills and mindset to become writers who shape meaning with clarity and intent. They learn to make choices that will affect their reader in an intended way. Many schools have reported an increase in pupils’ motivation in writing as a result.
So, what does Section 4 ask of us as teachers?
Here are the big takeaways I keep coming back to.
- Make thinking visible. Let children see the real decisions behind writing.
- Prioritise oral rehearsal and talk.
- Use reading as a model. Draw attention to how writers achieve their effects.
- Teach the craft of writing, not checklists. Help children develop choices they can select from purposefully.
- Hold purpose and audience at the centre. Everything the writer does should link back to intention.
- Embrace the recursive nature of writing. Build flexibility. ‘Writing is not a linear process, like following directions on a map.’
Section 4 offers a realistic, grounded acknowledgment of what it takes to help children become real writers. It recognises the complexity of writing and the need for explicit teaching, modelling, talk and authentic purpose. Most importantly, it values the process (the thinking) as much as the final product.