Childcare providers have a moral and legal duty to safeguard children from infections and illnesses. In England, hygiene is covered under Section 3: The Safeguarding and Welfare Requirements of the Early Years Foundation Stage (EYFS) statutory framework, updated in March 2017.

Section 3.54 requires providers to ensure that their premises are “fit for purpose” and comply with the requirements of relevant health and safety legislation. The framework specifies compliance with hygiene requirements.

So it goes without saying that correct and proper hygiene practises are very important when running a Nursery or pre-school. Unlike at home, a nursery or pre-school can be very susceptible to infections or illnesses. Proper hygiene control affects everyone at a nursery, Parents, Staff and the Children.

Promoting good hygiene also helps to educate children on hygiene practises.

Below are 5 simple ways to help stop the spread of infection in your reception class, nursery or pre-school.

1. Hand washing

It is vital to teach and consistently promote proper hand washing in your nursery or pre-school. It is important for both for staff and children alike. There should be enough suitable facilities to allow for thorough hand washing. This includes: a suitable wash basin with hot and cold taps, soap (not bars of soap), disposable hand towels and/or a hand dryer.

2. Identify germ-harbouring "hot spots," and clean them every day

Around 80% of all transferable diseases spread by touching. Frequently touched surfaces, like door handles, flushes on toilets, and cot rails provide an excellent breeding ground for germs and bacteria increasing the risk of infection spreading.

A wipe-down with a disinfectant cloth can help to eliminate germs before they have a chance to spread around your setting. This is important in high use areas or with places that are shared by many children.

3. Cleaning

Your nursery should have a cleaning schedule, which points out what should be clean, and how often as well as who is responsible for undertaking this duty. Certain areas will need more frequent cleaning than others. Proper detergent and disinfectant must be available, but caution should apply if children will be using items very shortly after being cleaning with chemicals. Carpets and rugs need to be included in your cleaning schedule. Don’t forget a process for sterilising toys that babies put into their mouth, these should be monitored closely and cleaned promptly before they are inadvertently shared!

4. Responding to infection outbreaks

Parents should be made aware that children who are unwell should be kept at home; this should be noted in induction materials and cited in relevant policies. Refer to guidance from Public Health, England and guidance from the DfE, when developing your policies and procedures.

• Health protection in schools and other childcare facilities

Those with a temperature and other specific signs and symptoms should be excluded until they are better (48 hours from the last episode in the case of diarrhoea or vomiting). Please refer to the exclusion guidance provided from Public Health

During any infection outbreak, increase environmental cleaning (especially toilets and door/flush handles) Reinforce good hand hygiene with children, especially after going to the toilet and before eating and drinking. Ensure toys are cleaned and dried after use. Exclude children with symptoms and advise staff members with symptoms to refrain from work until they have been symptom-free for 48 hours. Sand/Water and or play dough may have to be replaced as necessary.

5. Changing Children’s Bedding

If children are sleeping at your setting everyone should have their own set of bedding that should be laundered at least once a week. The frequency of washing should be increased if there has been an outbreak of an infectious illness or the child has been poorly bedding should be washed at a temperature of 60 degrees to ensure all bacteria is killed during the cleaning process.

The framework for teacher assessment of writing has changed. The ‘ITAF’ of yore is now the less catchy ‘TAF’ having lost its interim status and has a few notable changes to the ‘pupil can’ statements for each of the standards. Key highlights include handwriting being very much back on the agenda (rather than only being considered for judgements relating to Greater Depth) and a shift away from the ‘grammar/punctuation bingo’ checklist approach towards a more holistic composition and effect one.

One of the biggest changes you will have noticed is the addition of guidance relating to allowance for a pupil to a have a ‘particular weakness’ in their writing. Now, before we get too excited, the STA are quick and keen to point out that this is not a return to a ‘best fit’ approach at all. The model of assessing against the ‘pupil can’ statements is still very much a ‘secure fit’ approach (where pupils have to satisfy all of the statements), but just with some wiggle room – perhaps a ‘wobbly secure fit’, if you will.

Now what may feel slightly odd about this is that the regular ‘secure fit’ of the ITAF did always feel like it had some room for wiggling anyway. The qualifiers ‘some’, ‘many’, and ‘most’ already meant that it wasn’t quite an all-or-nothing approach, and those qualifiers remain. But nonetheless, there is now this further ‘wiggle’ in the form of the STA saying that, on occasion, one element of weakness shouldn’t prevent a pupil being awarded a standard where they meet all of the other ‘pupil can’ statements (see below for direct from the horse’s mouth)

• A pupil's writing should meet all the statements within the standard at which they are judged. However, teachers can user their discretion to ensure that, on occasion, a particular weakness does not prevent an accurate judgement being made of a pupil's attainment overall. A teacher's professional judgement about whether the pupil has met the standard overall takes precedence. This approach applies to English writing only.
• A particular weakness could relate to a part or the whole of a statement (or statements), if there is good reason to judge that it would prevent an accurate judgement being made.

So what does this mean? Well, in the training the STA rolled out to LA lead moderators just before Christmas, they emphasised that this is to allow the teacher judgement of a pupil’s achievement of a standard to overrule the meeting of every ‘pupil can’ statement in very particular cases where the teacher has good reason to believe that the standard awarded is the correct one and provided they can justify it in a moderation dialogue.

The examples STA gave, where one element or weakness should not interfere with the achievement of a standard, were always something very specific. It wasn’t the case of just writing off a whole ‘pupil can’ statement, but rather where a pupil just didn’t demonstrate a part of one or had a weakness that could potentially affect parts of a couple of statements.

It feels, initially, like this amendment may be addressing the issues we encountered for pupils who may have dyslexia/dyspraxia (or potential tendencies to those from a KS1 angle) and previously then lost out on the achievement of standards. But the STA did not state that as such, and in their examples they dealt with a range of possible ‘particular’ weaknesses, for example, a KS2 girl whose home language is German and so has an issue with the use of the possessive apostrophe (which is not generally used in her home language) still being able to achieve Greater Depth, or a KS1 boy whose writing was clearly meeting the Expected Standard but had a small issue with tense consistency.

It is worth mentioning that the materials we were given as part of the STA training for LA moderators are available on NCA Tools in the Teacher Assessment area.

It certainly does seem that this could be helpful for our pupils who have an issue specific to them that may otherwise be a barrier to their achieving what feels like the most appropriate standard. I can see how this could be useful for those children who perhaps have issues with tense or syntactical elements due to EAL, or patterns of spelling error due to dyslexia/dyslexic tendencies or indeed handwriting/motor skills.

What this doesn’t mean is that a whole class could have a particular weakness with spelling, for example. In the STA guidance it is clear that this isn’t a get-out-of-jail-free card. The STA used a helpful phrase to explain the ‘particular weakness’ – that it means a weakness in the achievement of the ‘pupil can’ statements, rather than a weakness in the child. It needs to be something very specific to that child’s writing and able to be justified with good reason during the moderation discussion. Also, this doesn’t change anything for children with physical disabilities. As in previous teacher assessment frameworks, allowances should still be made so that a disability that affects writing does not become a barrier for a child achieving the standard that fairly reflects their achievement.

In discussions with teachers at our recent Years1&2 moderation clusters, this alteration to how the ‘secure fit’ is to be executed certainly seemed to be welcomed. As much as it doesn’t allow as much flexibility as previously may have existed in the ‘best fit’ of NC levels, it does allow a more holistic view of a pupil’s writing to be taken into account by stepping away from a requiring a slavish adherence to ticking off everything in order to achieve a standard.

Writers can be great even with a particular weakness, and that is a message I am sure we can all get behind.

When thinking about the environment for our two year olds to play and learn we need to remember a few key factors. Two year olds need small spaces to be quiet and cosy as well as large spaces to use all their physical skills. They need to have many opportunities to engage in sensory activities; this encourages their natural curiosity and helps them to understand some of the possibilities of what they can do. They respond well to simple open-ended resources; and activities that focus on building concentration, problem solving language and skill building. It’s good to start by building on what they already know, what they need and what will hold their attention and imagination. Well placed supportive adults also play a huge role in getting the environment right for two year olds.

So definitely not as easy as it sounds.

If, in the last week or so, you stood back and watched a room full of children and adults all engaged in purposeful play, then chances are you understand what a good environment needs to have. If however, you have seen some children wandering around the room appearing unsure of what to do or play with; then reviewing your environment should be a priority.

A two year-old needs to see what is on offer at the beginning of play. The first thing to do is to make sure you are not confusing continuous provision with storage.

Look at these two photos of Maths provision for two year olds. Both are offered as part as an enabling environment for children to use. One is ready to play and one is not, so one is storage and one is continuous provision.

 

 

Storage: Many full boxes packed into a unit, often with a rug in front of it. When offering this type of provision, practitioners often say ‘the children can get out what they want’ but for a two year old this may mean lifting down a heavy box and then either tipping it all out or simply playing from what is in the top of the box. Offering resources in this way is not the most appropriate way to engage children in a rich learning experience as often, by the time they have the resources they want and got to a point of deep play, it is tidy up time or time for a story. It also relies on children being able to build a meaningful play experience out of a box of resources. Not a skill all two year olds have.

Continuous provision: accessible resources ready to play. Set up individually so that children can see what there is and what the starting point to play might be. Continuous provision allows children to select resources that are ready to use and set up to complement the area they are playing in. For example, this picture is of a small world continuous provision in a Hertfordshire nursery.

 

Notice how the resources are set up to complement the play. Therefore, if a child would like to add people to the train play, then they know where they are. Notice also that there is not a huge amount of resources on the shelf. No storage here. Just a select amount of resources. This way, both the children and the adults can focus on language and extending play.

It gets better!

Many of our Hertfordshire settings are moving away from offering predominately plastic to children. Instead, providing children with resources and objects from the real world.

 

Natural materials provide children with more tactile stimulation than plastic. They have different textures and smells. They also have a place in the real world, allowing children to make sense of their environment and link their own experiences through their play.

This quote from Margaret McMillan, a pioneer of nursery education, is over 100 years old, but is as true today as it was then.

‘Most of the best opportunities for children’s achievement lie in the domain of free play, with access to varied materials’. Margaret McMillan 1914

This means offering a variety, not just of resources but also of textures, possibilities, problems to be solved, excitement, motivation, curiosity, familiarity and challenge through real objects and natural materials.

So maybe it’s time to review your environment, tidy up and sort out your continuous provision to ensure all your two year olds are motivated to engage and learn.

Some of the photos used in this blog and many more can be found in the HFL Education publication ‘Places to Play for 2 year olds’.

This exciting resource complements ‘Places to Play for 3-5 year olds’ and shares good practice in several areas including the adult’s role, vocabulary, children's voice as well as many ideas for enhancing your places to play for 2 year olds, covering 20 areas of provision.

This is a question that comes up a lot – understandably: after all, if we are in the business of education then we are all about children making progress. But it is apparent that there still remains a variety of interpretations of that word ‘progress’. For many, many years, school leaders have been used to a systemic view of progress as being something that could be measured and expressed using numbers, and that these numbers could be used as evidence of school effectiveness at every stage in a pupil’s journey. The DfE and Ofsted changed their mind about this notion over 2 years ago now, but some school leaders still feel wary about letting go of their detailed data spreadsheets. Again, this is entirely understandable. It is a huge culture shift to move from the old world of constantly trying to convert learning into a numerical measure, to this new world where we talk about progress in a different way. But it’s a step worth taking, as I will explore in this blog.

Firstly, let’s try to define progress. As far back as 2018 (before the publication of the current Education Inspection Framework) Sean Harford (in this blog post) defined progress as “pupils knowing more and remembering more”. This is still the working definition used by Ofsted, and is supplemented by the view that the school’s curriculum is the progression model – i.e. the progress of learners is evident through exploring the journey that they are taking through a well-sequenced curriculum.

So we have shifted from a position of trying to measure progress (quantitatively) to trying to demonstrate progress (qualitatively). Or rather, a position where school leaders ultimately need to be able to reassure themselves that learners within their care are making progress through the curriculum, mainly for their own internal accountability, but also (occasionally) for external audiences.

There are just three points in time where we still attempt to express progress using numbers: once in primary school (KS2 progress scores) and twice in secondary school (Progress 8 at Key Stage 4, and value added measures at Key Stage 5). It is only possible to justify expressing progress numerically at these points in time because these measures are based on very large (national) datasets, where statistically valid correlations can be analysed, meaning that we can indicate, with a statistically significant degree of confidence, in which schools the progress made by learners was above average and in which schools it was below. At no other points in time do we need to try to express progress using numbers and attempts to do so are not worthwhile.

The question that we really want to be able to answer is ‘how well are children learning (the intended curriculum content) in this school?’  We have to accept the reality that it is never possible to truly and completely know the answer to this question with 100% accuracy. We can make good attempts at answering the question, but there will always be margins of error. This is because we can never know with absolute certainty what is going on inside the minds of learners. We use assessment to try to find out what children have learnt - the knowledge they have gained, skills they have developed and their ability to apply their knowledge and skills in various contexts. Some assessment techniques will be more reliable (and valid) than others when it comes to ascertaining the learners’ knowledge, but however effective that assessment is, it will always be a proxy for the actual learning. If we then try to boil down all our assessment knowledge into a grade or a number, we are losing even more accuracy and useful detail. So we might end up with a nice precise numerical progress measure, to several decimal places, giving an illusion of accuracy, but the reality is that it is not as meaningful as it might appear, in terms of answering our question ‘how well are children learning?’

It’s like taking a sentence written in English, translating it into German using a basic English-German dictionary, then putting that into an online engine to translate it into Swedish, then finally translating back from Swedish to English. It would not be surprising if the final result had deviated significantly from the original input. Some meaning might have been lost, or perhaps altered, so that it now implies something different.

Of course, I accept that, for my part, I have contributed to the ‘data machine’ over the years, helping to develop tools that schools could use for internal tracking and spreadsheets to analyse. At the time, schools seemed to need such systems and I was happy to help meet that demand. But now that the external need for data has gone, the opportunity really is there to re-evaluate what data we actually need - what is useful and serves a genuine purpose - and to strip away the things we don’t need or which are not helpful. In terms of the ongoing, day-to-day assessment which lies at the heart of good pedagogy, I discuss a range of important ideas in this blog: The place of assessment in the new Ofsted framework. As for data tracking systems, we definitely now advocate a ‘keep it simple’ approach (hence our Easy Tracking approach which we launched in 2020) - acknowledging that there is a huge wealth of assessment information that teachers will hold in their heads, derived from all their classroom interactions with learners, but that it is not necessary or desirable for electronic data systems to attempt to hold all such information. The most important purpose of this professional knowledge is that it should shape what happens next, i.e. teachers use the results of their assessments to either make necessary adaptations to the current lesson, or to a future lesson, or to the curriculum plan itself, or provide targeted support to particular learners. The ‘evidence’ that this is happening will be in the pupils’ learning outcomes.

As for tracking systems, the thinking behind our Easy Tracking approach is that it is a simple, light-touch approach to capturing internal summative checkpoint assessments: just enough to provide school leaders with the overview that they need, but without trying to imply a level of accuracy that would not be justified.  It should always be remembered that all this data does - all any data does - is provide a starting point for discussion. The numbers might indicate that, for example, attainment in maths in Year 4 is not quite where we would like it to be. But what does this mean? Can we deduce that this tells us that the teaching is not as good as it should be?  Of course not. We need to follow up and explore further before any firm conclusions can be drawn. We need to find out what assessment methods the Year 4 teachers have used, and how they have reached their judgements. Are their approaches consistent with other teachers across the school or do they vary significantly? We could explore for example (across all the classes in the school):

• what sorts of questions or activities have the teachers used to inform their assessment?
• how valid and reliable are these as assessment approaches, i.e. do they actually assess the domain of skills and knowledge that they were intended to assess (validity) and do they do so in such a way as to reliably determine the extent to which learners have secured that knowledge (reliability)?
• what was the timing of these assessment activities, i.e. how close to, or distant from, the point at which key concepts were directly taught? Does this show whether the relevant knowledge is in the child’s short-term or long-term memory?
• are the teachers looking for depth and application of knowledge, or a more surface-level regurgitation of facts?
• are the assessment activities closely matched to what the children should have learnt? (This would not be the case if, for example, a commercially produced test were used which included questions on topics not yet taught.)
• to what extent are gaps in pupils’ learning playing a part, where learners are at the ‘lower end’ of attainment? Are these gaps recent or from previous terms/years? How effectively are pupils supported to catch up?

The above list of questions is not exhaustive – it serves merely to illustrate that there are a great many variable factors underpinning any summative assessment.  Therefore it would be wrong to assume, from data alone, that we can deduce (for example) in which classes the most effective teaching is taking place.

There is an important message for school governors here too. Because governors are often not educational or curriculum experts, there could be a tendency to over-rely on numerical data as a means to monitor the effectiveness of the school. Again, data can play its part but is best seen as a conversation-opener, not as the be-all and end-all. “I noticed the data seems to show that…” is fine, as long as that is seen within the context of a line of enquiry, that needs to include gathering further information, e.g. talking to curriculum leaders, talking to children about their learning, asking children to show them their work and discuss what they learnt from an activity.

Children with Special Educational Needs

A genuinely frequently asked question is how best to evidence progress for children with SEND, especially within the context of our Easy Tracking system, where a child might be categorised as working at ‘Pre-Curriculum Expectations’ year on year. It is not possible to infer from that data whether the progress that child is making in their learning is acceptable, good, excellent – or not good enough. But the truth is, it was never really possible to make those judgements from data, even when we were using measurable P-scales or other tools. The reality has always been that, particularly amongst this group of learners (although you could argue this is true for everybody) each individual is completely unique. Their needs, their barriers to learning, are so completely unique that no ‘one-size-fits-all’ approach to defining ‘good progress’ numerically has ever been appropriate.

Just as is the case for all children, to be able to comment on such a child’s progress, we first need to have established what the curriculum expectations are, based on where they are now and where we are trying to get them to in the future. This might mean discussing appropriately ambitious curricular targets relevant to the child, perhaps thinking about the small steps and goals that we might want them to achieve across the next 6 weeks, say. And then reviewing the learning to see whether those goals have been achieved. That is what progress is all about. What could be considered slow progress for one child might be considered phenomenal for another, taking into account that child’s particular context. Attempts to produce a system that would quantify such progress seem both unworkable and unnecessary.  Once you accept that fact and embrace the reality that progress can only be described qualitatively, in curricular terms, it frees us up to focus on what really matters: using really good formative assessment to establish exactly where each child is in their learning now, and then planning really good teaching that is matched to the children’s needs, to get them to where you need them to be.

Progress versus attainment

Putting all this talk of progress to one side, what we really need to be striving for is (at least) expected standards in attainment for all learners. One of the main arguments against the previous system of levels, sub-levels and point scores, was that it was possible for a culture to develop where we just focused on all pupils making a certain amount of progress (whether that be defined as ‘3 points’ or something else) and thinking that was ok. The result of this of course was that attainment gaps remained (and still remain) wide. A pupil working behind the expected level of attainment at the end of Year 3, say, could make the ‘expected amount of progress’ (whatever that is) across Year 4, but would still end the year behind where we ideally want them to be and could be forever chasing their tail – never quite securely achieving what is expected of them. Our aim ought to be that the curriculum in each year of learning equips the children with the knowledge and skills that they need to be able to successfully access the curriculum for the next year. We must therefore shift the focus of ‘Pupil Progress Meetings’ to become ‘Pupil Progress & Attainment Conversations’ and ask ourselves important questions, such as

• in which aspects of the curriculum are each of these children secure?
• in which aspects are they less secure?
• what specific measures could be put in place to try to enable these children to achieve the Expected Standard? (e.g. more practice in…, focused teaching on…, addressing gaps in…)

Ultimately, for the future life chances of our learners, attainment is the key.

Signs of spring… snowdrops blossoming, evenings becoming lighter and preparation for transition! At this point of the year, allocations for the new starters are now in process and by the time the Easter holidays have ended, parents/carers will be finding out which school their three- and four-year-olds will start in September. That means, early years practitioners will be beginning their juggling act of continuing to provide high quality provision for their current cohorts and be carefully monitoring the children joining them in the autumn term.

At this point, it is worth reviewing transition procedures to ensure there is sufficient time put aside to fulfil the induction, setting and home visits, taster sessions, stay and plays and numerous admin tasks that are required to enable smooth transitions. Where settings have children moving to school, it is beneficial to have conversations with parents/carers about transition and contact schools to exchange valuable information.

“Creating a smooth transition into school is vital to ensuring the child gets the best possible start in their new setting.”

Developing a smooth transition into school, Early Years Careers, 2016.

Here are a few things to consider when reviewing and planning the procedures in place to support smooth transitions for every child.

 

Top tips to support smooth transitions into school

1) Develop a transition timetable and make the whole school/setting aware of it

Transition procedures need to be robust and everyone involved should have sight over events/activities that are planned. It would be beneficial for early years leaders/managers to compile a list of the procedures involved with transition and plot them against the annual planner for the whole school/setting, such as when visits to feeder settings or stay and play sessions are scheduled. This will ensure that transition is embedded in practice, acknowledged by everyone, and establishes a clear expectation that every child will have a successful start to school.

 

 

2) Exchange meaningful information between professionals

Many of the children joining the school will have attended a previous setting or childminder and it is vital that time is set aside share information about the child and family. It is important to remember that some children may have been with the previous provider from as young as three months old and others may have only been with the provider for a term. Conversations between professionals will enable valuable information to be shared which will ensure appropriate provision is put into place to meet the needs of every child.

 

 

3) Build relationships with the families

“For Early Years settings, partnerships between parents are every bit as important at the end of their relationship as at the start.”

Hello, Big School – Managing transitions, Melanie Pilcher.

Many will be saying goodbye to early years practitioners that have cared for their child for a significant amount of time and they need to establish a trusting relationship with the next professional. Regardless of home background or circumstances, positive relationships must be formed. Parents/carers can be just as, if not even more, anxious about their child(ren) starting school, and as you will be aware, parents/carers are their child’s first and most important teacher. They will be able to provide you with a wealth of information about their child(ren). In some cases, children may have only been cared for at home, therefore gathering this information is even more pertinent. It can be very daunting for parents/carers to welcome teachers/practitioners into their homes. View home visits as a privilege that many are not privy to.

 

 

4) Plan and organise the learning environment to meet the needs of all children

The information gathered from conversations between professionals, parents/carers and children should be used to inform planning and organisation of the learning environment for the when the children start. Ensure that children’s interests and needs are catered for by reviewing the provision and making enhancements that will make children feel welcome. 

‘When small changes are supported by responsive, knowledgeable adults, children will gradually discover that their world is a safe and predictable place’

Seamless Transitions – supporting continuity in young children’s learning, DfE.

5) Be prepared for anything

Even with all the careful planning and preparation that are put in place, situations will always arise that were never expected. This would be great time to reflect on the procedures that have been put in place for supporting smooth transitions and to identify any developments that could be made. There will always be surprises and bumps along the way, unknown children will appear and staffing may well change but if effective transition procedures in place these can be referred to whenever required.

 

 

“A successful transition means children settle quickly into school, learning and developing from day one.”

Transition to Reception, Anna Ephgrave, Teach Early Years.

The key thing to remember with transition is that it is not an event, it is ongoing and will require personalisation for individual needs to be met effectively which will allow children, and adults, to settle into their new surroundings and routines. Information gathered prior to children starting will provide an insight into where adaptation may be required and will enable schools to be fully prepared for their new starters.

To ensure a smooth transition is facilitated, the Transition Level of Need Tool (TLoNT) has been used successfully through Hertfordshire and continues to support practitioners and teachers to meet the needs of new cohorts.

 

This blog concludes our series of blogs based on the KS2 2022 SATs papers. In the previous two KS2 blogs, we have explored the similarities and differences noted between the content and expectations of the 2019 and 2022 papers.

In this blog, rather than comparing papers and questions, instead we will focus on how we might use questions (or any reasoning questions) to teach and develop children’s reasoning skills.

You may have had a chance to read Nicola Adams’ blog published yesterday and unapologetically, what we explore here directly piggy backs on the ideas shared. If you haven’t had a chance to read it, please don’t be put off by the fact that it has a KS1 focus as the strategies and skills discussed are highly appropriate for KS2 children.

When working with teachers and children, it will come as no surprise to you that when asked about what type of questions are preferred, both groups often talk to us about strengths within calculations or questions presented in arithmetic formats but are less confident when tackling worded scenarios where increased reasoning is required. This isn’t a new finding. As my colleague, Siobhan King, writes in her blog from 2019,

‘Sometimes I think we can be guilty of expecting pupils to learn how to reason by osmosis.’

So, what practical steps can we take to support children with developing their reasoning and problem-solving skills?

It may be tempting to revisit the mnemonic RUCSAC to help children with the steps needed to solve problem solving and reasoning questions:

• read the question
• underline the key words
• choose the operation/s to use
• solve the calculation
• answer the question in context
• check that your workings and answer make sense

The problem with this is that children can very often slip up early on with these steps and so then the whole process stalls. 

Instead of this approach, I will use the same approach that Nicola described in her KS1 blog, with a couple of tweaks for KS2, and exemplify it using 2 questions: 1 that is suitable for use with lower key stage 2 pupils and one more suited to upper key stage 2.

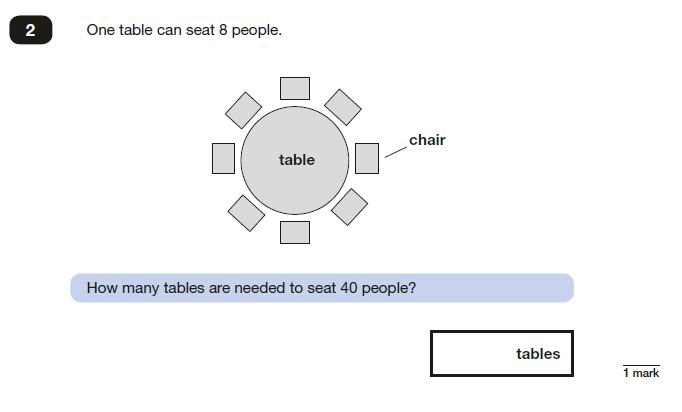
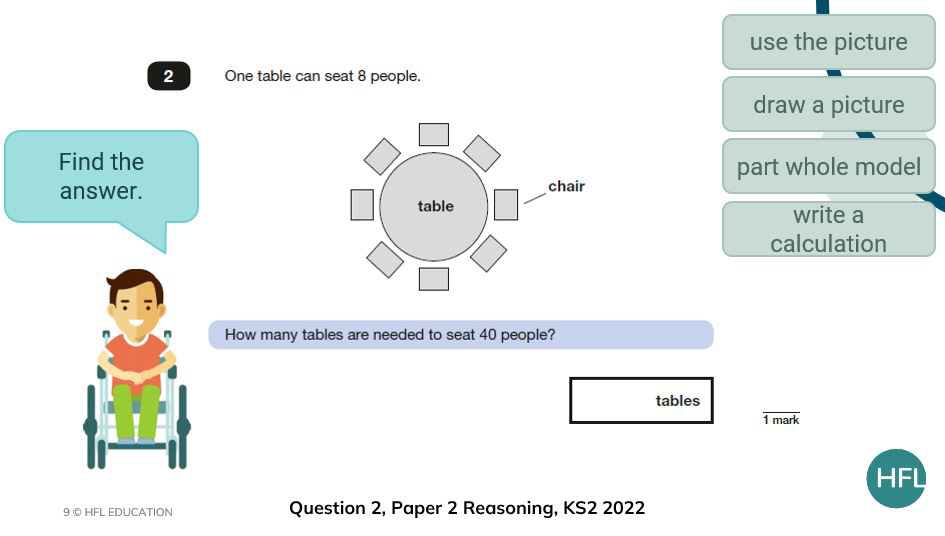
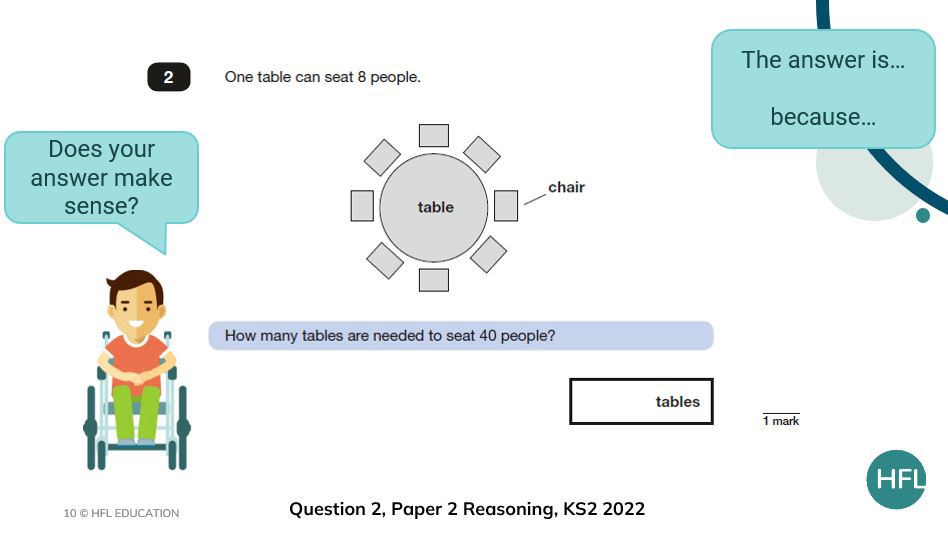
I have chosen the questions based on their content domain reference from the SATs mark schemes. Question 2 of paper 2 is referenced as 3C8/3C6 (multiply/divide mentally and solve problems using calculations).

 

 

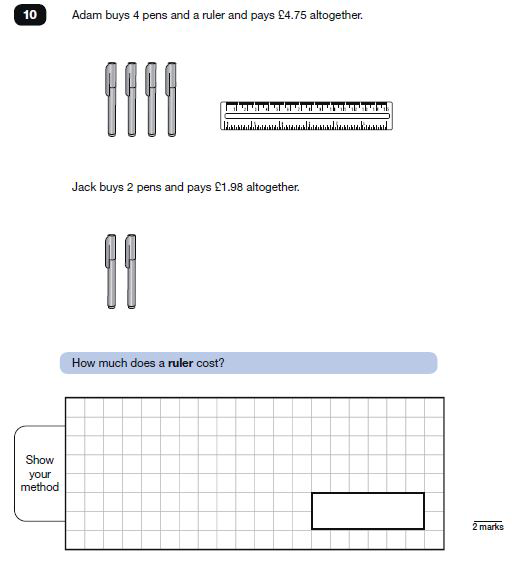
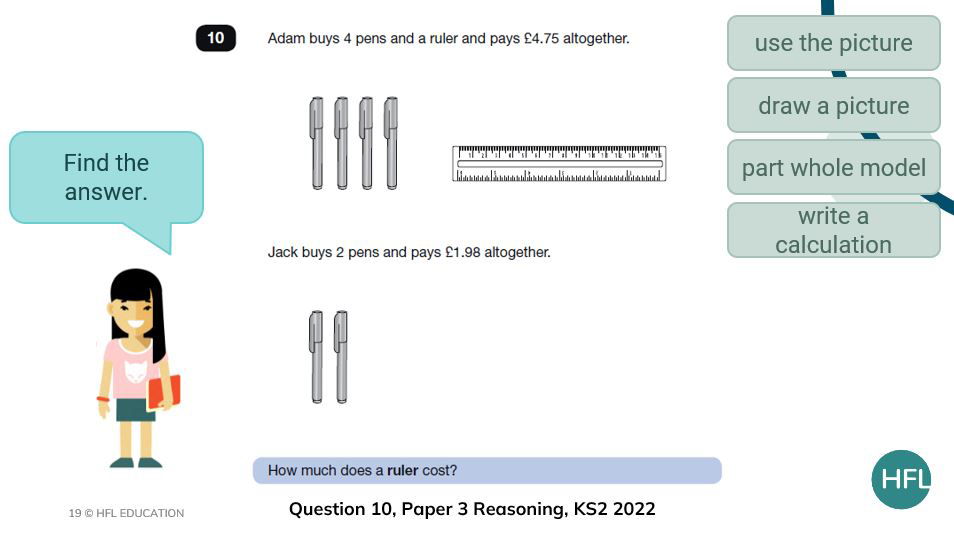
Question 10 from paper 3 is referenced as 5M9a/6A4 (solve problems involving measures and tackle number sentences involving two unknowns).

Just a quick caveat here – if you are using the content domain references to consider the pitch of specific questions, it is also useful to note that the complexity of the expected response can elevate the challenge of the question.

 

 

Step 1: Direct pupil focus

To begin with, remove as many distractions as possible from the question and decide what we want to draw the children’s attention to. This may depend on the chosen question as to what information you choose to start with. The important thing here is reducing possible anxiety and potential information overload. We want to slow the children down. In both the examples below, all text has been removed from the questions but sentence starters have been provided as a starting point to the question, ‘What do you notice’.

 

 

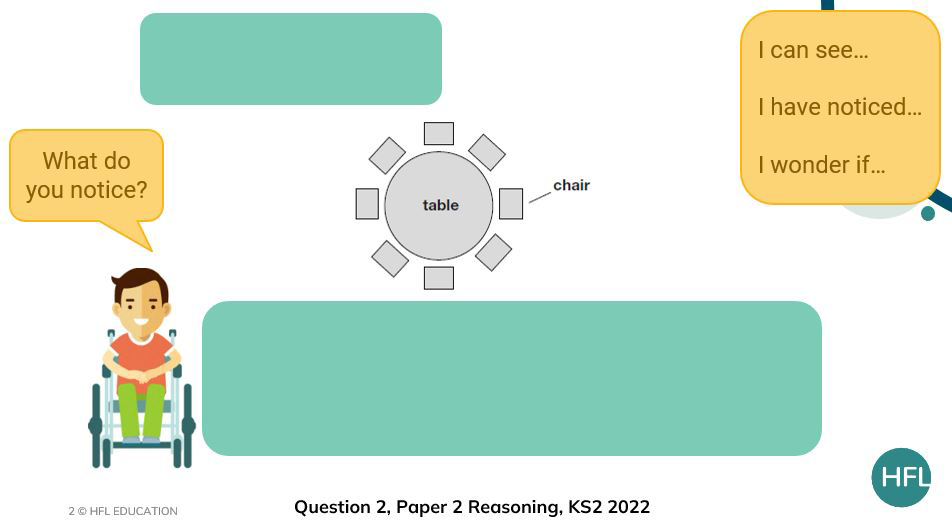
Children should be encouraged to discuss what they can see and what they notice in pairs, in small groups or as a class. Included here is also the sentence stem, ‘I wonder if…’ which could either be presented with the other sentence starters or be added after.

The initial observations may be simple and that is fine. We want all children engaged and talking and so any response goes!

Step 2: Refine pupil thinking

Following the initial conversations, we then want to encourage children to ‘filter’ and refine their thoughts.

To do this…

• provide a list of key vocabulary
• expect pupils to articulate their thoughts in full sentences
• ask pupils to listen to others to see if they can add more details or be even more precise

 

 

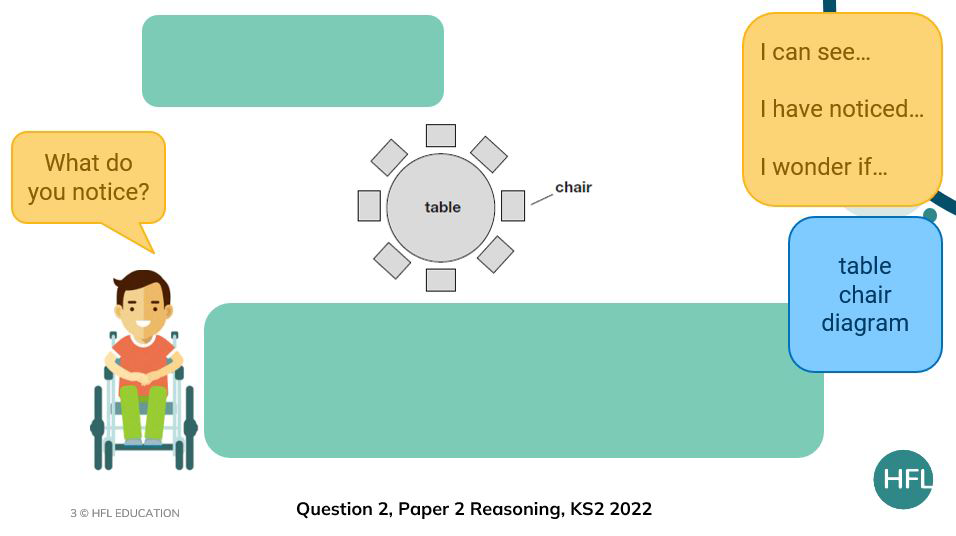
With question 2, the vocabulary list may be simple and draw attention to the fact that a diagram has been provided as opposed to literal pictures of tables and chairs.

 

 

 

With question 10, two examples have been provided to show how the vocabulary could be layered during pupil discussions.

First, I would want them to consider simply what they can see in both the top and lower image and then I would want them to start comparing the images.

Do they notice that there are double the amount of pens in the first image than the second?

Can they talk about the unequal groups that they can see?

This will be important later when the question is finally revealed and so these are points that I want to draw attention to beforehand.

Step 3: Build on what they know

To do this…

• reveal information from the question bit by bit
• after each reveal, ask the pupils, ‘What do you know now?’
• ask pupils to suggest any additions to the vocabulary list

 

 

 

 

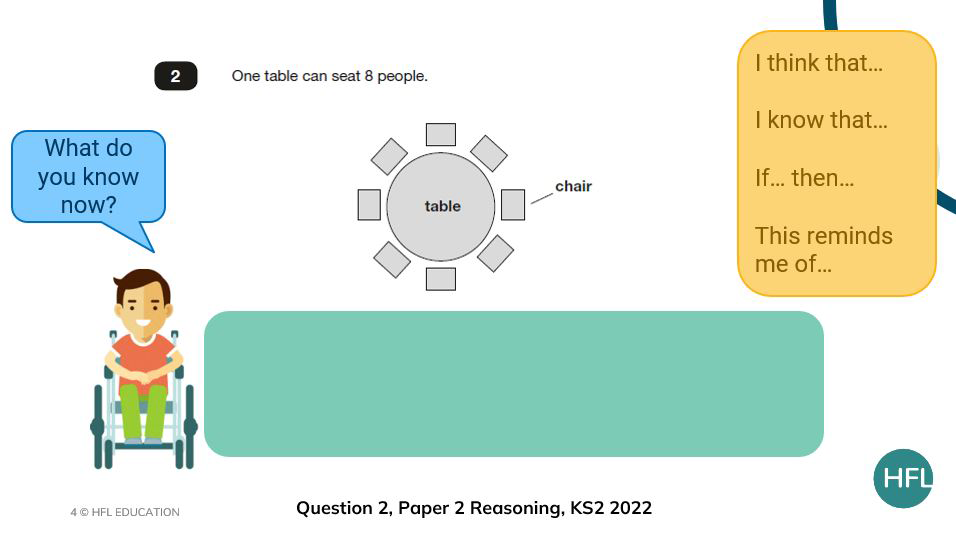
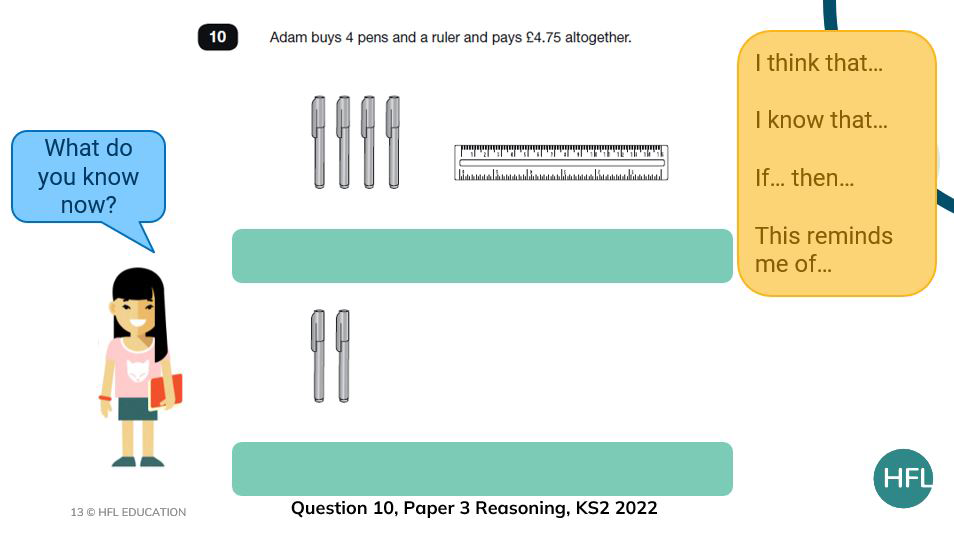
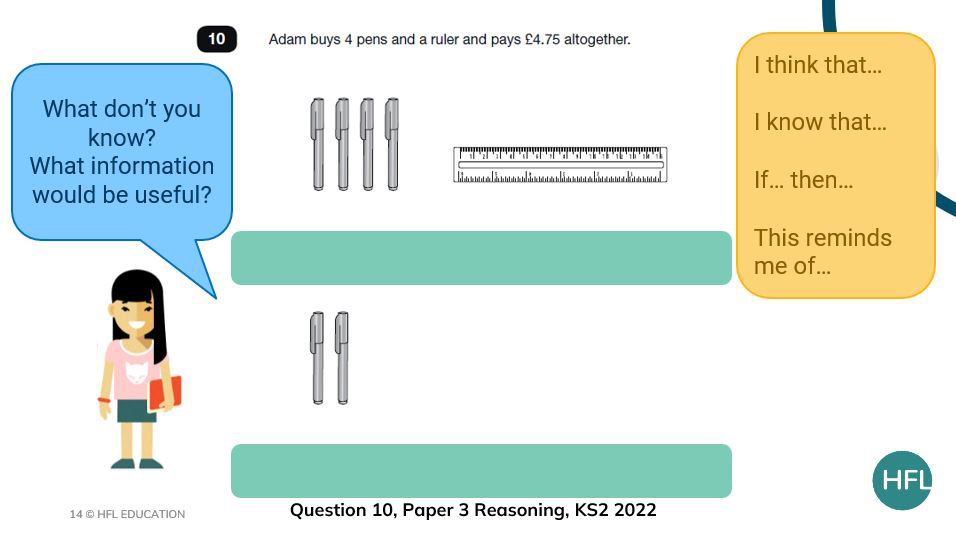
The revealing of information is always my favourite part of the teaching sequence especially where there is additional information to reveal such as in question 10.

Asking the children what information they would like to know or find out encourages them to think about associating different information with parts of the question.

For example, at first, we know how much the 4 pens and the ruler cost altogether but it would be very useful to know either the cost of a pen or how much the ruler costs as we are dealing with two unknowns here. I tend to ask the children if they are ‘ready for more information’ to build the suspense!

We can also continue to use the initial sentence starters but also encourage children to make links with real life experiences and other learning by including the stem, ‘This reminds me of…’.

For question 2, children might be thinking about sitting in the school dining room or thinking about equal groups for games in PE as examples. Again, this focus is important as later on the children will need to be thinking about equal groups to solve the actual question – they just don’t know it yet!

 

 

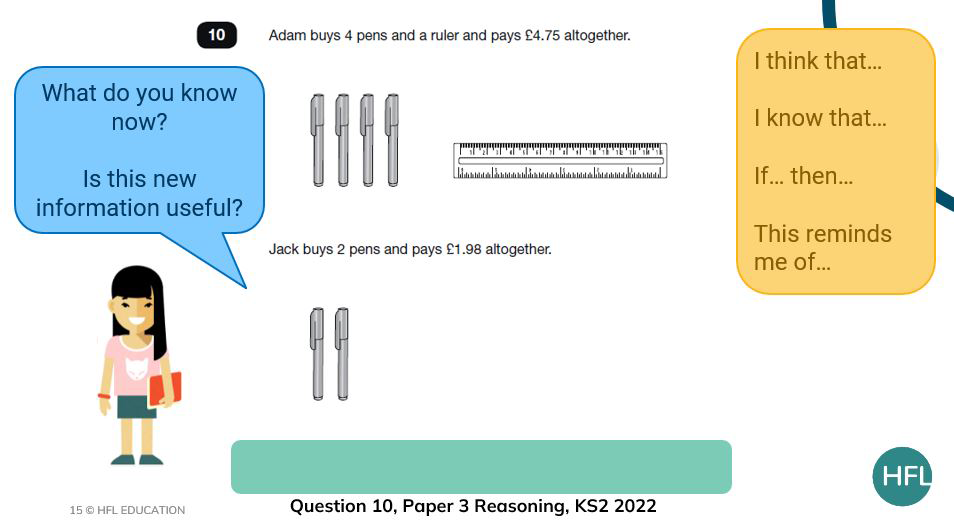
Asking the children to compare the initial information with the added information and to assess the usefulness of this new information adds to the challenge for those who are ready for it.

Step 4: Consider ‘the question’

To do this…

• BEFORE revealing the question, ask pupils, ‘What could the question be?’

This allows you as the teacher to assess whether the pupils are considering the likely structure of the problem. Using a vocabulary bank, whether this is the same as the initial bank, or with some additional words added can be a useful opportunity to further refine children’s thinking.

 

 

 

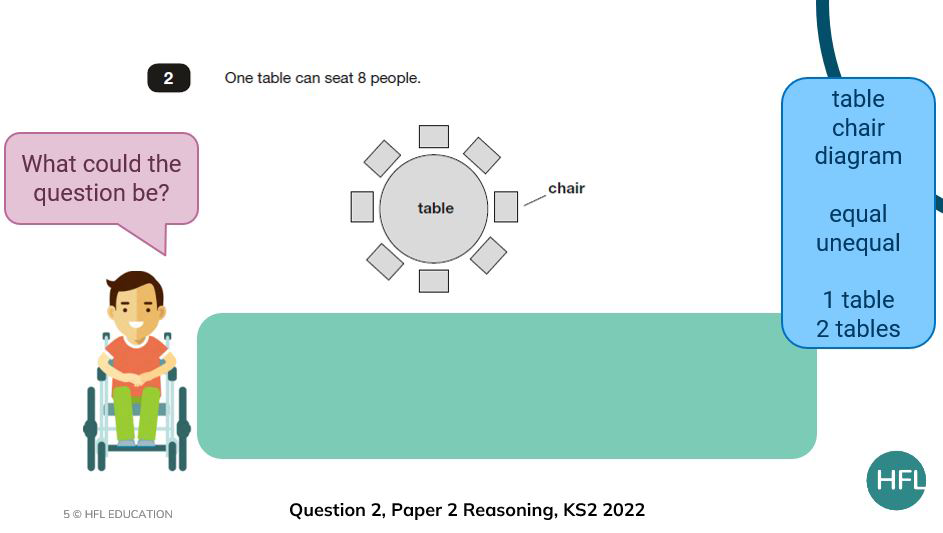
In this example, are the children considering questions that would involve multiplication, division, and equal groups such as in the scenarios they may have been talking about using the sentence stem, ‘This reminds me of…’

If a child came up with a question such as, ‘How many children could be seated at the table if we took one chair away’ (which should still be a valued question), this would tell us that they have not considered the vocabulary of equal and unequal in the word bank nor the mathematical domain that this image or related situations would allude to.

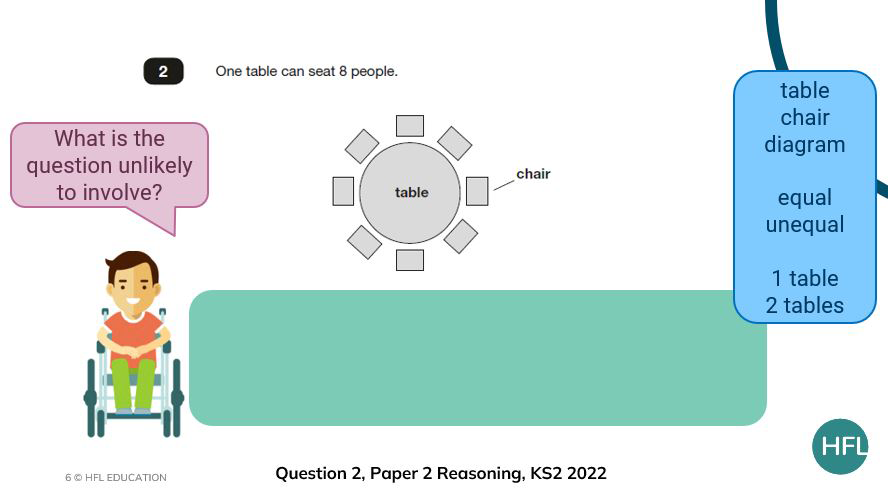
Furthermore, asking the children to consider what is not likely to be included in the question provides a challenging opportunity for children to think about the choices that they have made when considering this question.

 

 

In this example, children might suggest finding the total cost of 6 pens and 1 ruler which, again, would be a valid and reasonable question and could lead to an interesting discussion. For that question, would we need to know how much the ruler costs on its own?

Step 5: Reveal ‘the question’

 

 

 

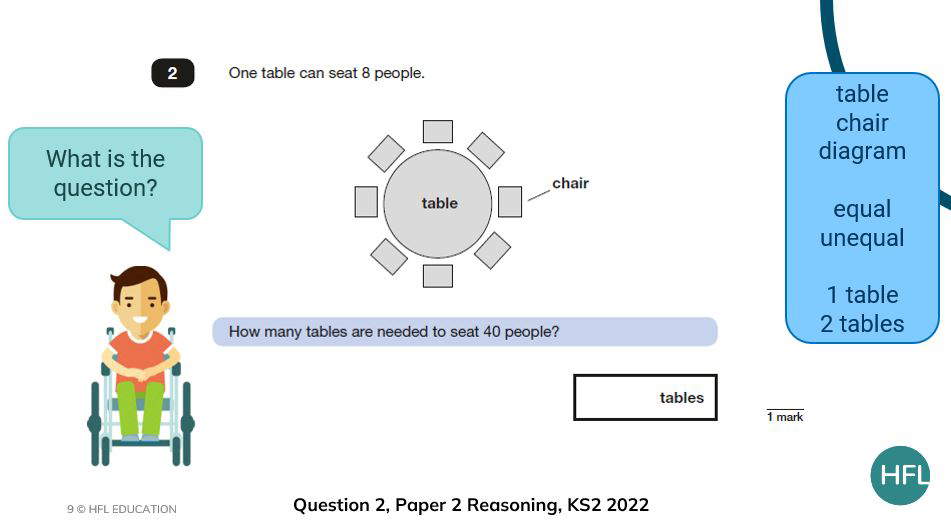
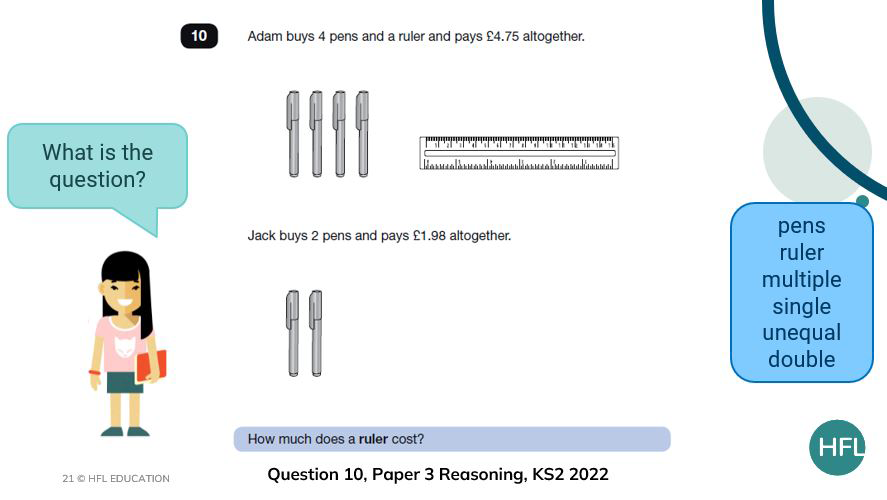
To do this…

• ask children to read the question aloud. Perhaps read it aloud as the teacher and then ask children to repeat it back
• ensure children understand all of the words within the question and link this to the model and vocabulary list if needed

Step 5: Reveal ‘the question’ – a simpler example

It may be that you want to take the opportunity to simplify the question when you first reveal it to encourage all children to access it and not be put off by the numbers used in the ‘actual’ question.

In the example below, instead of seating 40 children, I want the children to firstly think about seating just 16 children. I want them to do this to draw attention to the fact that we are working with equal groups of 8 and connect division and multiplicative scaling.

I would tie this in with the next step – representing the problem – and explore how we could represent this by annotating the diagram, drawing a bar model or listing calculations for example.

From here we could then ask them what if we have 20 children? Do they consider the fact that 2 tables will be needed for 16 children but there will be 4 children left who will need another table. You could then reveal the actual question and children could apply this thinking to 40 children.

Is the final question easier or harder than when we thought about 20 children?

 

 

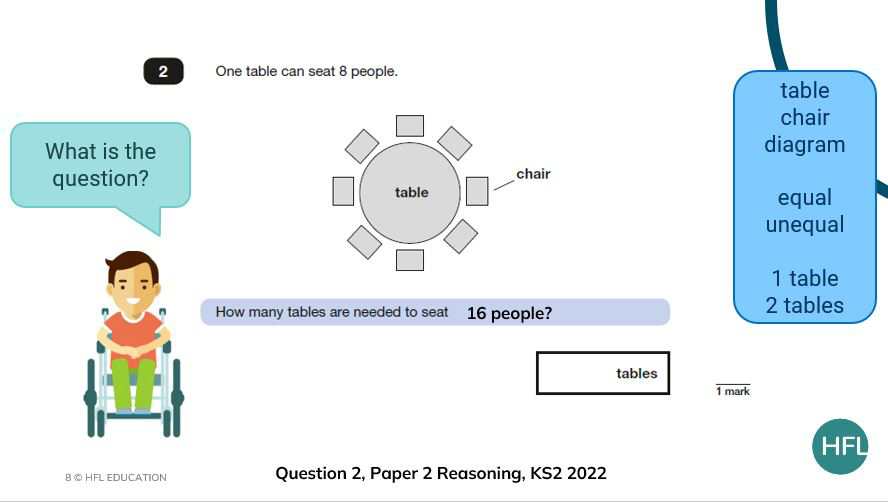
Step 6: Represent the problem

By this point, we are beginning to consider the calculations needed to solve the problem at hand. For some, considering one representation is challenging but important in supporting them to ‘choose’ the operations needed. Whereas for other children, encouraging multiple representations can prove challenging as we may be asking them to think further than their default method.

To do this…

• ask the children, ‘How could we represent the problem?’
• be specific about representations – ‘What would it look like as a drawing?’, ‘What would it look like as a bar model?’, ‘What would it look like as a calculation?’
• ask the children to compare their representations to a partner’s. Can they see where each part of the problem is shown? Can they explain their representation or model to someone else?
• support children to make connections by modelling and comparing representations. Can they match bar models to appropriate operations?

 

 

 

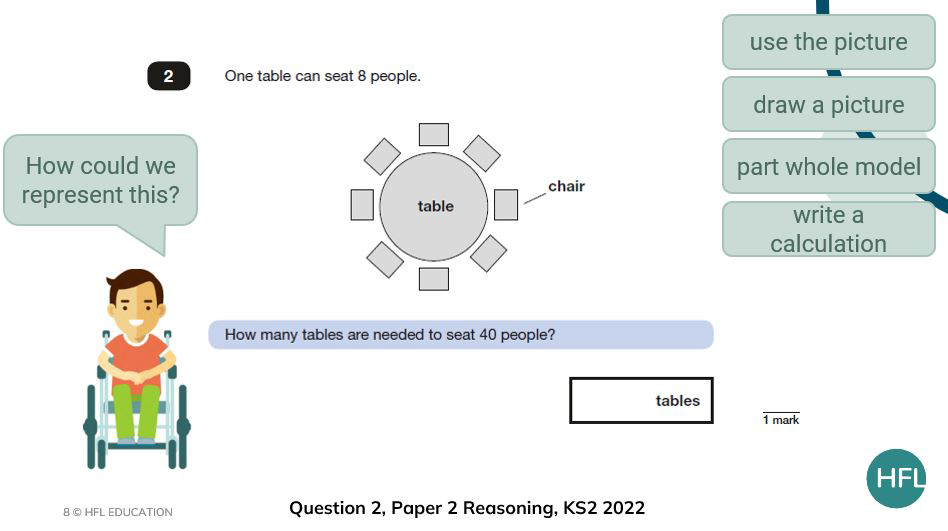
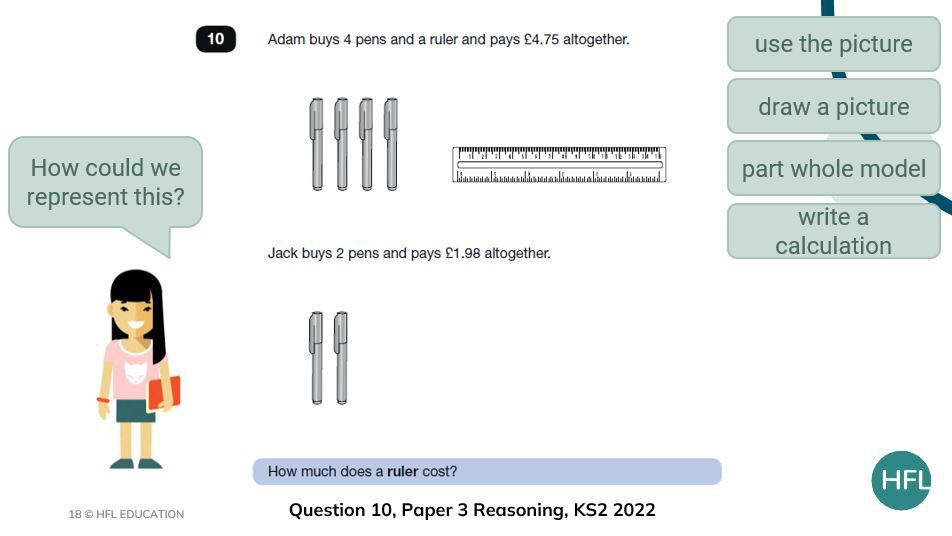
So far, there has been an emphasis on talk and discussion and now, it would be useful to ask children to use jotters or mini whiteboards to draw their representations. They can then use these to explain and compare with friends as well as providing adults with opportunities to ‘mark’ over the shoulder and draw out misconceptions which could then be shared with the whole class.

 

 

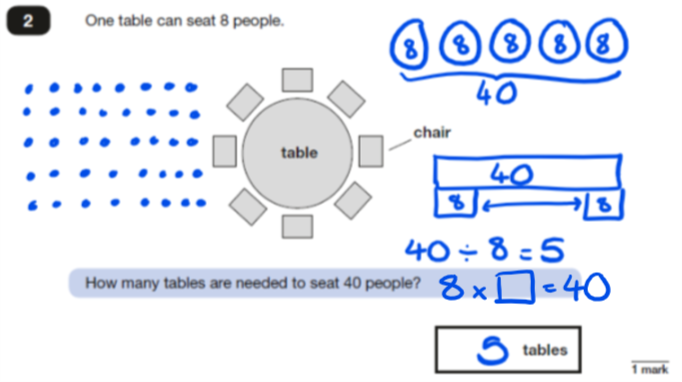
Some children might represent the problem by using an array and 1:1 correspondence and skip count in 8s to keep track of when they reach 40 people. These children should be encouraged to identify the group size (8 people) and then number of groups (5 tables) to check that they are using the correct structure for the scenario.

Children might also recreate the table image by drawing groups of 8 where they have moved away from requiring 1:1 correspondence while other children might represent the problem using a grouping structure bar model, identifying that they are looking to find how many groups of 8 can be made from 40. Children may then use these models and representations to write an equation to show which operation they will use to solve the problem.

 

 

 

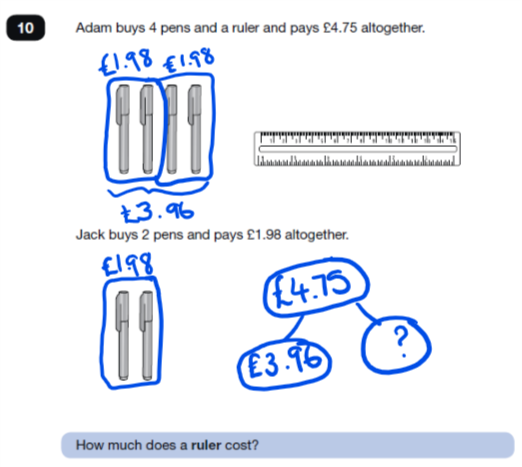
Children might choose to draw on the images provided before writing any equations such as the first example where they have identified that to find the cost of 4 pens, the cost of 2 pens could be doubled before subtracting this from £4.75. Alternatively, they may choose to draw and write straight into the given answer box if they have been provided with copies of the question.

As when the children were discussing what the question could be, all of the children’s representations and models should be shared and celebrated.

Step 7: Find the answer

To do this,

• ask children to identify on their representation where the answer is shown
• ask, ‘Have you identified the operation needed?’
• ask, ‘Are there different ways of finding the answer?’
• ask, ‘What could go wrong when you are finding the answer?’

 

 

 

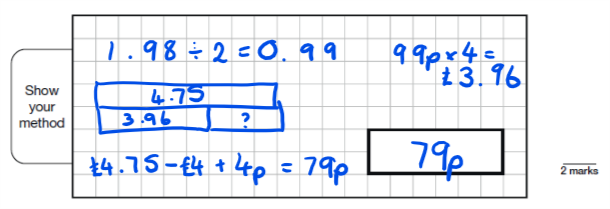
Again, at this point children should be given the opportunity to write down their answers including any jottings or drawings that they make alongside. Examples could be explored under the visualiser, and these could include successful examples of workings out as well as any errors which can then be discussed as a class.

For example, for question 10, do children double £1.98 using equal sum (£2 x 2 – 4p) before subtracting this from £4.75 or do they use a less efficient method of finding out what one pen costs and then multiplying by 4 before subtracting?

For question 2, which children choose the correct operation and divide 40 by 8 but skip count incorrectly or use an inefficient method for division?

Step 8: Check the answer makes sense

How often do the children down pens or move on after they have written their answer?

How many times do they groan at their ‘silly’ mistakes?

This step provides the perfect opportunity to slow down and check that answers make sense.

To do this…

• Consider all the information the pupils used while problem-solving (the image, the vocabulary provided, the key words in the question, any models or drawings)
• Ask the children to complete the sentence, ‘The answer is … because …’

 

 

 

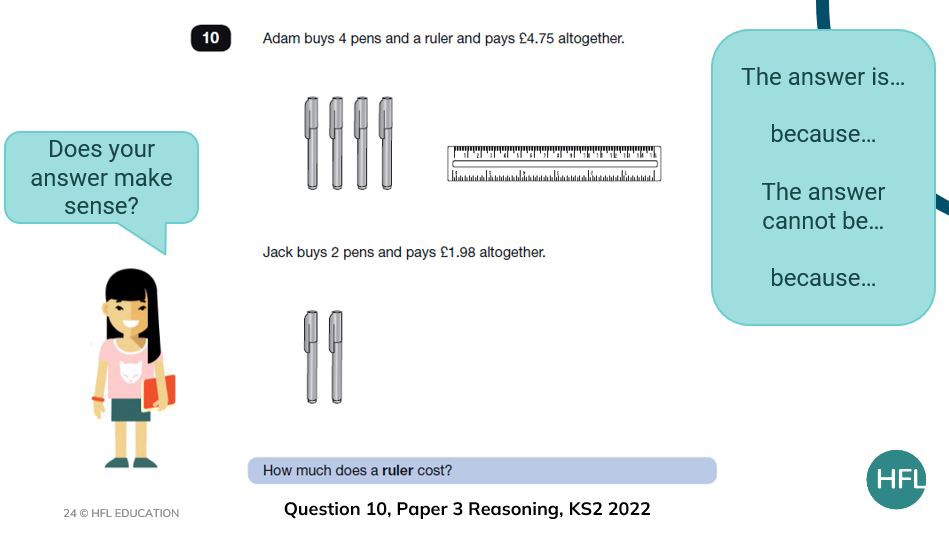
Adding in the additional sentence starter ‘The answer cannot be… because…’ allows misconceptions already discussed to be used by the children or the children to consider their own misconceptions whether they have made an error or not.

Further exploration – getting the most out of the question!

If appropriate, further exploration of the scenario could take place.

For example, children could go back to their initial responses to, ‘What could the question be?’ and answer these. Are they easier or tricker than the actual question?

Or a variety of ‘what ifs’ could be delved into.

For example, what if the answer to question 2 was 7 tables? What could the question be? How many different options are there?

Or for question 10, what if the unknown was different? What if we were told how much pens cost and how much a ruler costs but we had to find the change from £5 for 4 pens and a ruler? Or what if division was banned for question 2; how else would you solve it?

There are so many possibilities for continuing to explore the questions.

Developing independence in solving problems

What we would like to see over time is pupils developing more and more independence in using skills and ideas from these steps to solve problems themselves.

When planning a sequence of teaching and learning, refer to the SATs papers for questions that it would be opportune to drop in, either in the way outlined above, as a teaching opportunity, or as an independent or paired discussion task to allow assessment of how pupils tackle them.

This will also provide crucial information about which of the steps the children tend to find the trickiest. Is it articulating what they notice in full sentences? Is it drawing a model to support with choosing an operation? Or is it something else?

Whatever the sticking point, this can form the focus of teaching going forward.

There are plenty of past papers from which to choose questions and these can be accessed here:

• Key stage 2 tests: 2022 mathematics test materials
• Key stage 2 tests: 2019 mathematics test materials
• Key stage 2 tests: 2018 mathematics test materials
• Key stage 2 tests: 2017 mathematics test materials

Further reading

How to use the KS1 reasoning SATs papers to teach children problem-solving skills 

References

• Mathematics test framework: National curriculum tests from 2016 for test developers
• 2022 Key Stage 2 mathematics paper 2: reasoning
• 2022 Key Stage 2 mathematics paper 3: reasoning

Contains material developed by the Standards and Testing Agency for 2016 and 2022 national curriculum assessments and licensed under Open Government Licence v3.0.

Returning to school may, for some children, be a time of stress, disturbed routines and separation anxiety and there will be a need to adjust to a new type of school day. Children may be faced with repeated hand-washing routines, a new type of fire-drill and social distancing. Their friends may be in a different classroom or may be coming in to school on different days.

In this article, we will look at some iPad apps that can be used to support children at these times, particularly those with additional needs and SEND. We will focus on calming, sensory apps and using the wide functionality of iPads to create Social StoriesTM to help some children adjust to the new routines and situations they will face.

Calming apps

The iPad, with its touch-screen and small, personal design, is ideal for many children who may benefit from interacting with apps that calm, engage and absorb the user’s attention. A great source of this type of app is Sensory App House where a wide range of free apps are on offer for iPad, Chromebook and other devices via a browser (web apps.)

Sensory Plazma (from Sensory App House). This is like a digital lava lamp where the wax bubbles can be manipulated by touch. A range of onscreen buttons change the colours and visual effects as well as triggering sound effects, although, of course, the iPad can be muted if this is a distraction.

Sensory Mica (from Sensory App House). This app responds to sound, creating bright, engaging visual effects when the user makes noises. The visualisations can be changed and sound-sensitivity adjusted.

Fluidity HD (from Nebulous Design). A wonderful, free (with in-app purchases) app where the user can watch and interact with relaxing, swirling patterns. A powerful range of settings means the visualisations can be customised, and sounds enabled or disabled.

 

 

Using iPads for digital Social Stories(TM)

The concept of Social Stories was designed by Carol Gray in 1991 as a strategy for improving the social skills of those with Autistic Spectrum Disorders. Through Social Stories, information is shared with the user through a description (the ‘story’) of the situations or events taking place that the user will encounter, often with descriptions of why things take place. The stories describe an event or social situation, how others may feel in the situation and an appropriate response.

Social Stories are:

‘Short descriptions of a particular situation, event or activity, which include specific information about what to expect in that situation and why’

(The National Autistic Society 2014)

Social Stories can be reassuring at times of anxiety and can provide a routine response to particular situations. They are generally short and use simple, clear language. They can be used repeatedly over a period of time and phased out as the need lessens. Therefore, they may be helpful to some pupils/students who are struggling with the return to school, or the changes to the way the school day will need to run with social distancing measures in place. Social Stories will often follow this format:

 

 

For more information on creating Social Stories, please see the National Autistic Society website.

Carol Gray’s website includes some ready-made printable stories designed to help users understand the Covid-19 pandemic.

There is no need for a Social Story to be digital, but by utilising photographs and videos, it may help the user better understand the situations and what to expect. The iPad has a built-in microphone, stills and video cameras, so it is easy to capture footage and bring it all together using a story or book-making app. There are several of these apps available. Perhaps the best known is Book Creator from Tools for Schools Ltd. It is also available as a Chrome app.

Book Creator provides an easy platform to capture photos, video and sound, and place them on a digital page along with text, shapes, drawings and more. With Book Creator, authoring begins with a single button, from which a wide range of media can be added to the page. If the author is following the format above or similar, a different page can be used for each stage of the story and may include, for example, a photograph of a new classroom layout, handwashing or a video of people talking to each other from a +2m distance. Of course, the media you use would reflect the very particular situation that the child is having difficulty with.

 

 

In addition to its ease of use, Book Creator has the advantage of offering multiple export formats, making finished stories widely accessible on different devices, or printed if preferred, though of course a print-out cannot include video or sound.

Therefore, a social story could be shared with the family of the child for whom it was created, to be used at home, as well as in school.

 

 

Supporting transition

At a time of school transition, creating talking/picture books can also be helpful in preparing children for their new environment. These could be created by the receiving school using the same technology that could be used for digital Social Stories, and shared with the feeder school. Children in the feeder school could also use such apps to create profiles of themselves, which could be shared with the receiving school.

There are plenty of ways to create stories using iPads, with different apps offering different levels of functionality. Other examples include:

Little Story Creator. Add photos, drawings, text and sound recordings to the digital page. The app is available for free, with in-app purchases.

Keynote. Apple’s powerful presentation app can be used for creating digital stories. Add photos, videos, text and more to the slides, using a new slide for each page of the ‘book’. Completed stories can be shared as PDFs or Powerpoints or accessed within the Keynote app on the iPad or Mac.

Chris Carter is an Apple Distinguished Educator and Book Creator Ambassador.

But aren’t they too young?

That is something I often hear in relation to the discussion and inclusion of LGBTQ+ themes in primary school. There are myths that by exposing young children to LGBTQ+ themes that it could harm them or make it more likely that they will themselves identify as LGBTQ+ as they get older.

‘Even before reaching secondary school, prejudice and discrimination can have a profound impact on young LGBT people’

 Hidden Figures report, LGBT Foundation, 2020

I would not for one moment ever suggest labelling any child as LGBTQ+, certainly not at a primary level (nor at a secondary level unless the child self-defines). Labels can be dangerous and force people into a box. When I was getting to grips with my sexuality as a teenager, the label was my biggest issue. In fact, when I first went to university, despite already being out to the majority of my school friends and family, I made the decision not to come out until after my first semester because I was adamant that I did not want my new friends to make assumptions about me based on the label of being gay.

Giving labels is not the place of an educator, however, what is our place – more than that – our duty, is to present to children all the ways in which people may decide to define themselves, and present that not only as acceptable, but as usual and as a valued part of our society. In a 2020 Hidden Figures report by the LGBT Foundation, statistics show that 70% of young LGB people have thought about taking their own lives. This rises to 92% for trans young people. The report states that: ‘The sustained impact of experiencing discrimination at a young age is indicated by the poor mental health outcomes for many young LGBT people’.

So, if a primary school chooses to ignore the existence of LGBTQ+ people within society by not including explicit reference to them within the curriculum, then – in my opinion – they will be having a direct impact on a child’s current and future mental health and wellbeing. This may also have a direct impact on the child’s academic success, therefore their future career options. Schools should be safe places for children and safeguarding is at the heart of everything we do, so why is it that in 2022, many schools are still choosing to avoid the issue as much as possible – largely due to fear of parental reaction perhaps? Or perhaps staff are scared of saying the wrong thing?

Is it also not reasonable to assume, that if by ignoring and failing to usualise (not normalise – that infers there is a way in which we can be abnormal) LGBTQ+ people in the curriculum, we are not only allowing mental health issues to develop but that there could also be an impact on behaviour? I was recently talking to a friend of mine whose daughter is now in secondary school and identifies as gay. Despite having a very strong family unit and attending a good school, this child displayed many challenging behaviours throughout her time at primary school and these got worse through the early part of secondary school culminating in some severe mental health issues. This has all been related to the fact that she now identifies as being gay. I have a question: if she had seen LGBT+ people in characters and books from an early age, if LGBT+ people had been included and usualised in the curriculum at school, would her behavioural issues have been so bad and would her mental health be in a better state today than it is currently is? One can only speculate, but I would guess that she has always felt different but didn’t know how and was unable to articulate that. Had she have seen herself represented at a much earlier age and seen herself as being ‘normal’ and a valued part of society, perhaps many of the issues which she has experienced and the behaviours which she has displayed could have been different.

If I think back to myself as a child, I always knew I was different – from a very early age. I can remember back to when I was at pre-school and I knew then that I was different from the other boys, but I didn’t know how and there was no way I could articulate that. Unfortunately, Section 28 prohibited schools from even talking about the existence of gay people throughout my time in school. Consequently, in my school reports, the overwhelming thing that comes across is that I was quiet and showed a lack of confidence. Recently, words used to describe me by colleagues included: outgoing, brave and engaging. This is quite a turn around. Undoubtedly much of that will be due to age – I am sure many people grow in confidence with age. However, would I have been more confident when I was at school if I could have been my authentic self? I knew I was different. I didn’t know how for a very long time. The other children knew I was different – they probably didn’t know how either. Some were perfectly fine and were my friends. Other chose to bully me because I was different. Would they have acted differently if we had been taught about the existence of LGBT+ people from an early age? Would I have had more confidence in myself at school as a result? Perhaps this might have even had an improved impact on my academic performance – I would say now that I probably did not reach my potential. There are no sure ways to answer these questions, however, what I am sure of, is that there is a direct link between the usualisation of LGBTQ+ people from an early age and improved mental health of LGBTQ+ young people as they grow older, because they can see themselves being a valued part of society, no matter who they are.

It is now a statutory requirement for primary schools to include LGBT people within relationship education. Statutory government guidance tells us that ‘At the point at which schools consider it appropriate to teach their pupils about LGBT, they should ensure that this content is fully integrated into their programmes of study for this area of the curriculum rather than delivered as a stand-alone unit or lesson’. Read the full text here:

Gov.UK: Introduction to requirements

 

 

I would argue that the point at which it is ‘appropriate’ to teach about LGBT+ people is from as soon as they step through the door. And this should happen not just through lessons specifically about relationships, but through the entire curriculum. In January, I spoke at the HfL Primary English conference focussed around diversity. I spoke about the outcomes of the Explore & Engage unit, ‘And Tango makes three’ by Justin Richardson and Peter Parnell. This is a great example of how LGBTQ+ people can be usualised through the curriculum. This book, if you don’t know it, is a story based around two male penguins – who are in a relationship – adopting an egg and raising a chick named ‘Tango’. This was written as an English unit of work which would work across the entire primary age range and provided a range of writing opportunities.

 

 

This allowed for teachers to assess children across a range of writing and to see progression across the school. This was an English-focussed unit of work which many schools across Hertfordshire used brilliantly and achieved fantastic outcomes with. The key for me though is that this unit did not focus on the same-sex element. It was there and discussions may well have taken place in classrooms if they needed to, but it was not the focus of this plan at all. This is what usualisation looks like. The inclusion of LGBTQ+ characters, threaded throughout the curriculum without that being the main focus. If this were carefully planned, across all the curriculum areas to account not just for LGBTQ+ people, but diversity in its entirety, then throughout their time at primary school, all children should get to see positive representations of themselves and their families throughout the curriculum. 

 

 

Obviously, this can then be supplemented with additional books which are read, unplanned conversations and discussions which will come up. It would also make additional events such as LGBT history month or Black history month more relevant and less tokenistic. A chance to really draw attention to that area, but not being something on a ticklist to say that that has been covered that year. We are fortunate that there are now an increasing number of fabulous books which show diversity in all its forms. Children’s books for all ages which can act as fantastic starting points for units of work, particularly in English. But how about other areas of the curriculum – surely there are ways to talk about diversity when thinking of artists, musicians, scientists, sports people just to name a few. Seeing these positive role models could be so empowering for all children and I think that we need to spend more time considering the role models which we use in our curriculums to reflect the society in which we live.

 

 

The point is to create an atmosphere and curriculum where anyone is accepted and valued, no matter who they are. If we can do this, the impact could literally be saving lives. What is more important than that?

With thanks to Longmeadow Primary School in Stevenage and Mary Exton Primary School in Hitchin for sharing these outcomes with us.

If you would like to speak further with Michael in relation to the content of this blog, you can email him at this address: migray@gamlingayvp.org