Bar modelling continues to prove itself as a powerful tool for making sense of complex mathematical scenarios. In this instalment of our SATs-focused bar modelling series, we turn our attention to Paper 2 of the 2025 KS2 maths papers, with a particular focus on questions involving measures.
Our previous instalments on this are also still well worth a read – we think so at least!
Find them here:
- KS2 SATs: the power of the bar model (2018)
- The power of the bar model part 1: Year 6 SATs 2024 reasoning paper 2 – questions and answers
- The power of the bar model part 2: Year 6 SATs 2024 reasoning paper 3 – questions and answers (2024)
Measures questions often combine multiple strands of mathematical understanding. Units, conversions, powers, operations (+ – x ÷) and reasoning can all be explored within a single context. For many pupils, this can feel overwhelming. But when bar models are used to represent these problems visually, they can help children to clarify relationships, identify what is known and unknown and ultimately give them the confidence to choose appropriate steps and calculations to solve the problem.
In this blog, we will explore how bar modelling can support pupils in solving measure-based questions, drawing on examples from the 2025 maths SATs Paper 2. As always, the emphasis is on exposing the maths, not just solving the problem.
We will look at how the language of part and whole, developed from early years onwards, continues to underpin pupils’ thinking- even in the most challenging contexts.
Example 1:
2025 KS2 SATs – Mathematics Paper 2, question 11
Bar modelling to expose the need for addition and subtraction
In this first question, a bar model can be used to clarify what we already know and what we do not yet know. This can help the children to identify the calculation(s) needed to solve the problem:
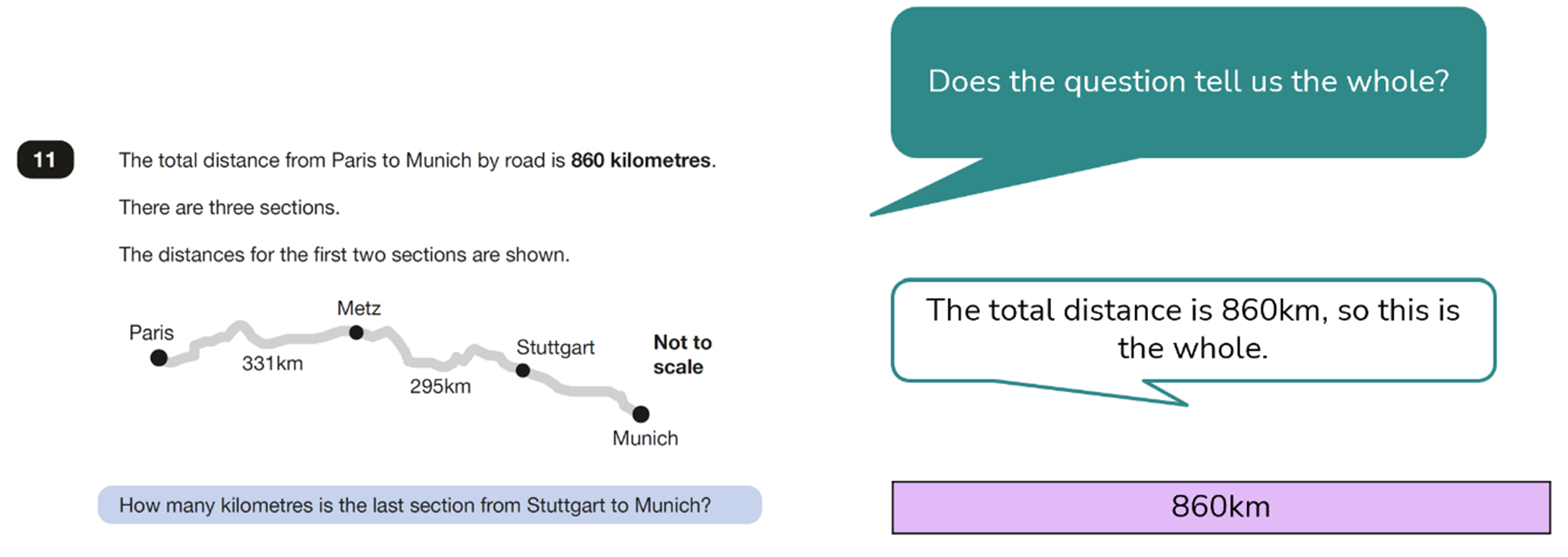
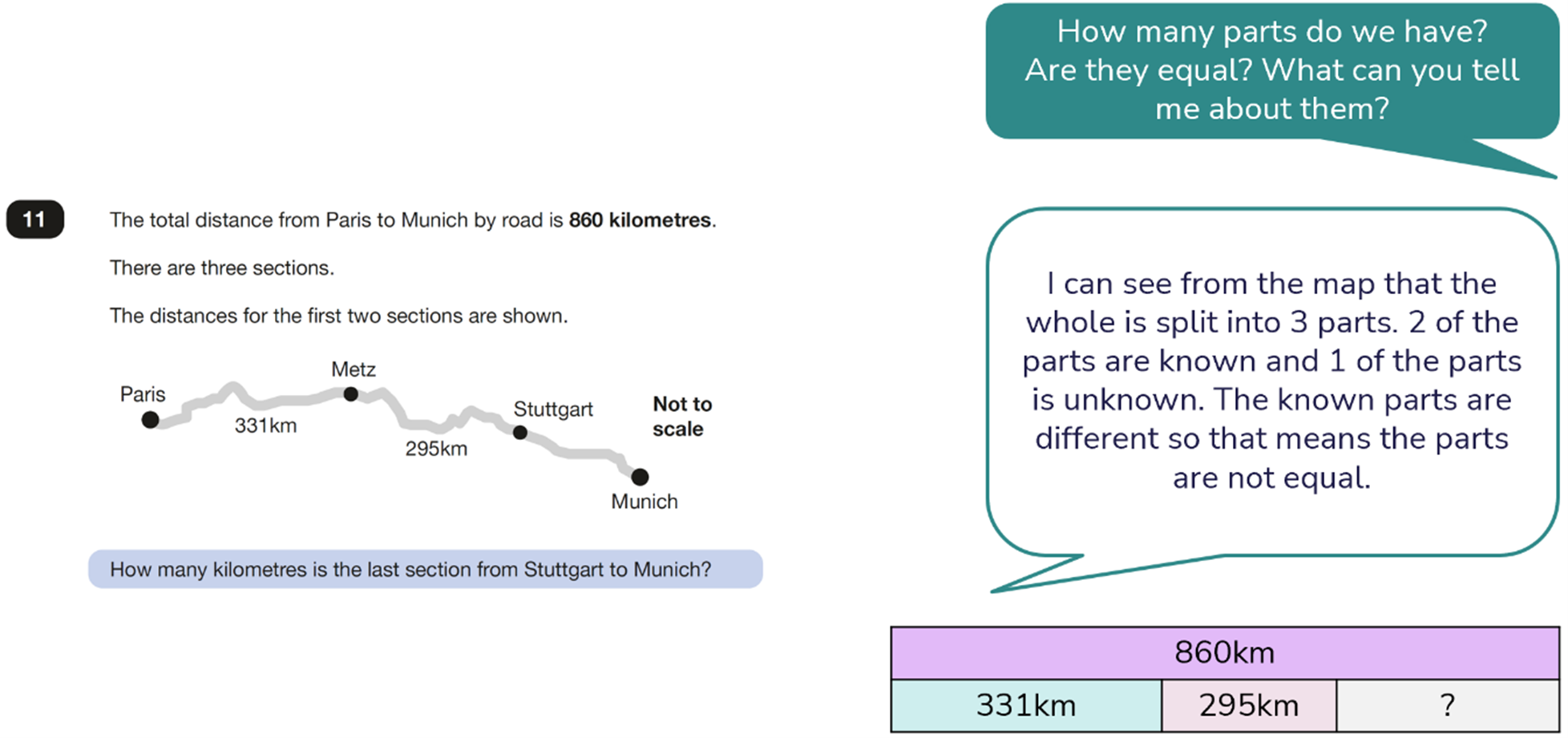
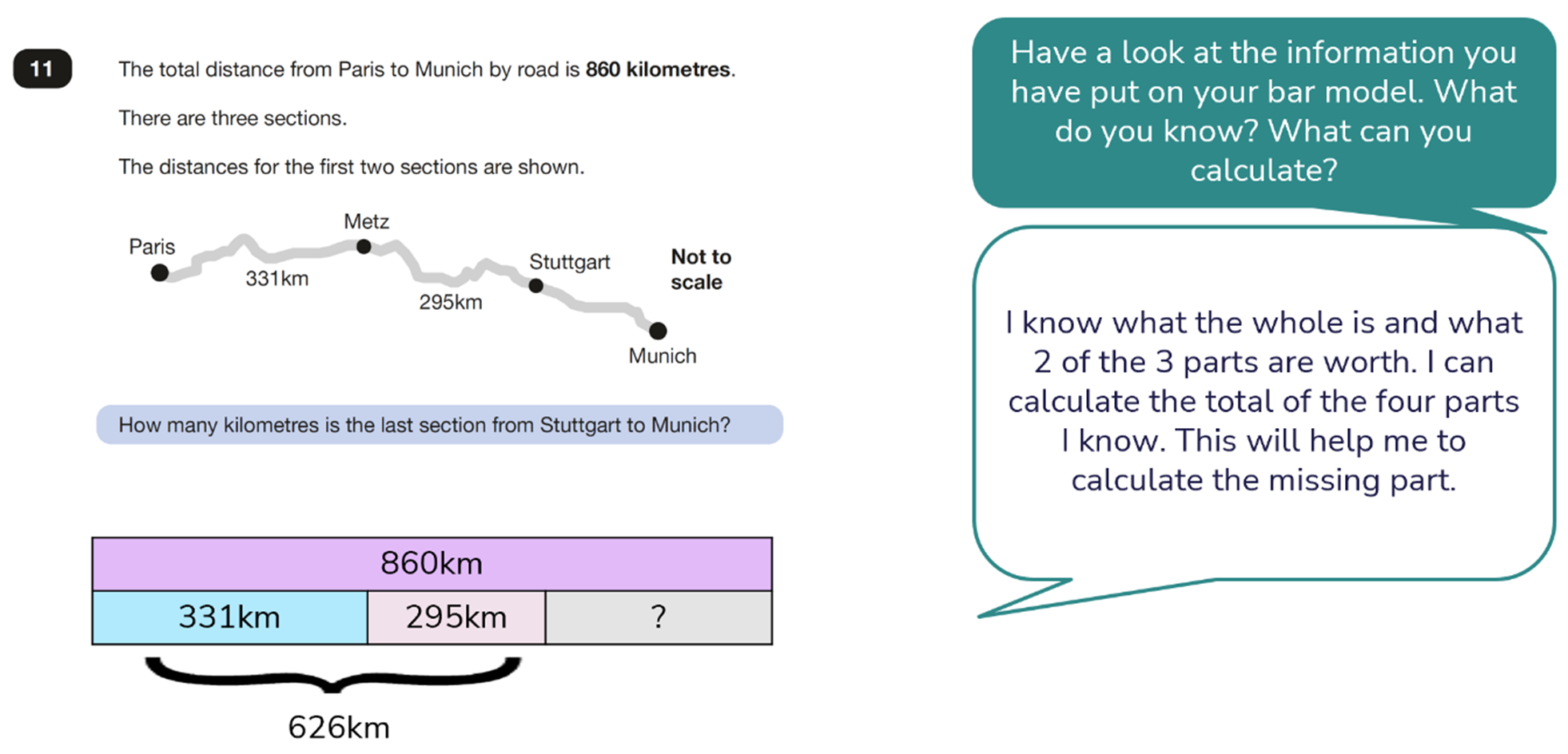
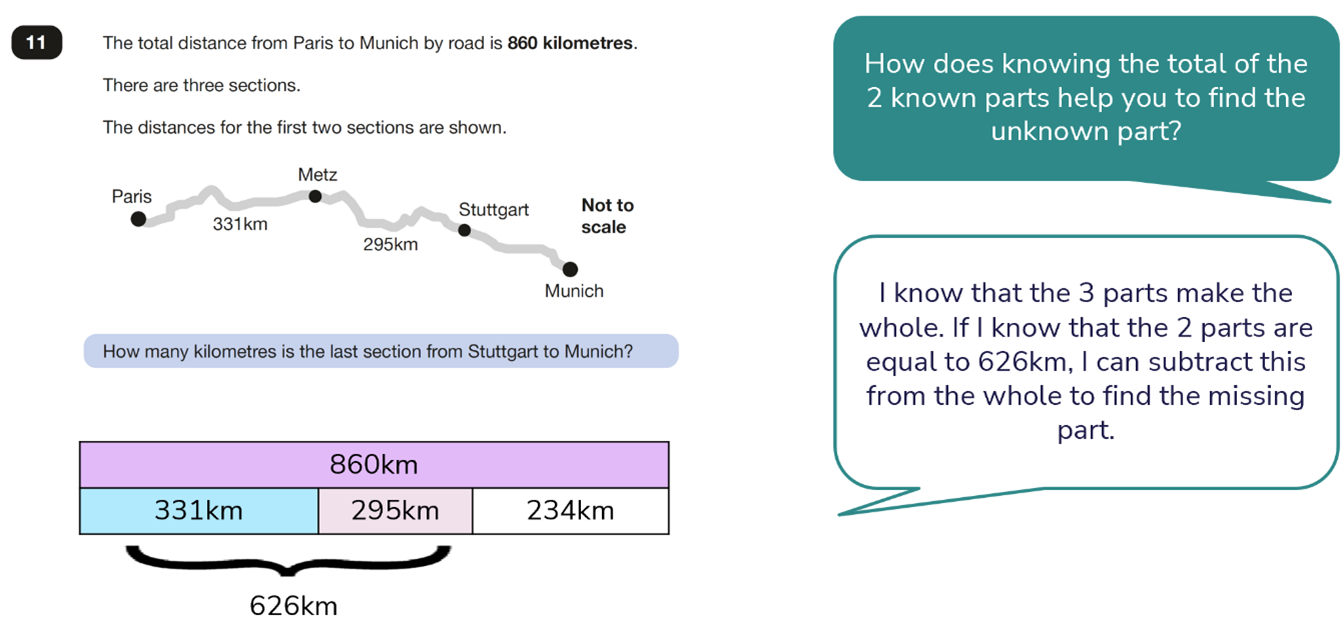
Solution:
The number of kilometres from Stuttgart to Munich is 234km.
By using a bar model to expose what is known and what is not yet known, it enables the children to identify calculation(s) required to find the missing part. In this case we can use addition to combine the known parts and then subtract this from the whole to find our missing part, as shown in the modelled talk above.
Example 2:
2025 KS2 SATs – Mathematics Paper 2, question 14
Bar modelling to expose the need for multiplication and addition
In this question the information is shared in a data table format. This requires the children to be able to extract helpful information first (reading the table) and then know what to calculate. In this question there are many parts which could present a challenge, and the children are required to find the whole.
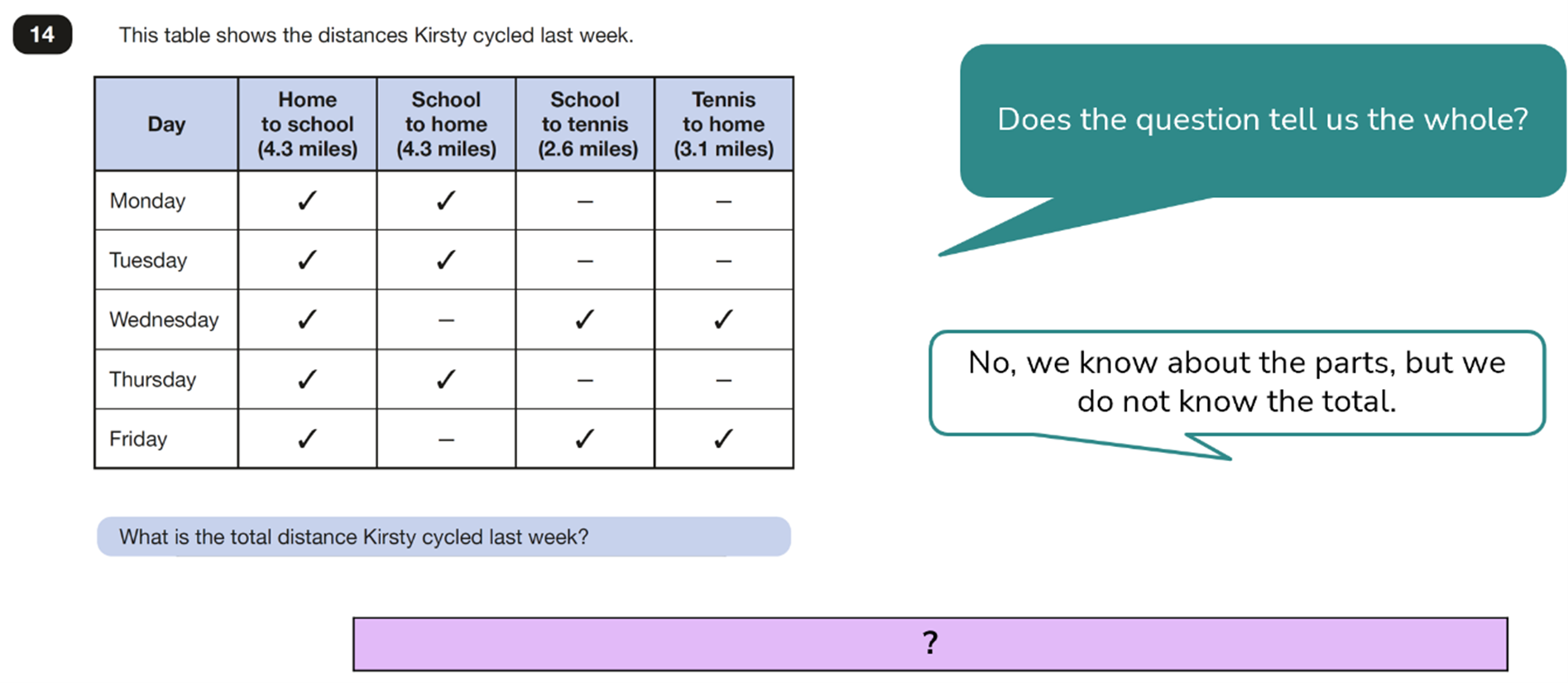
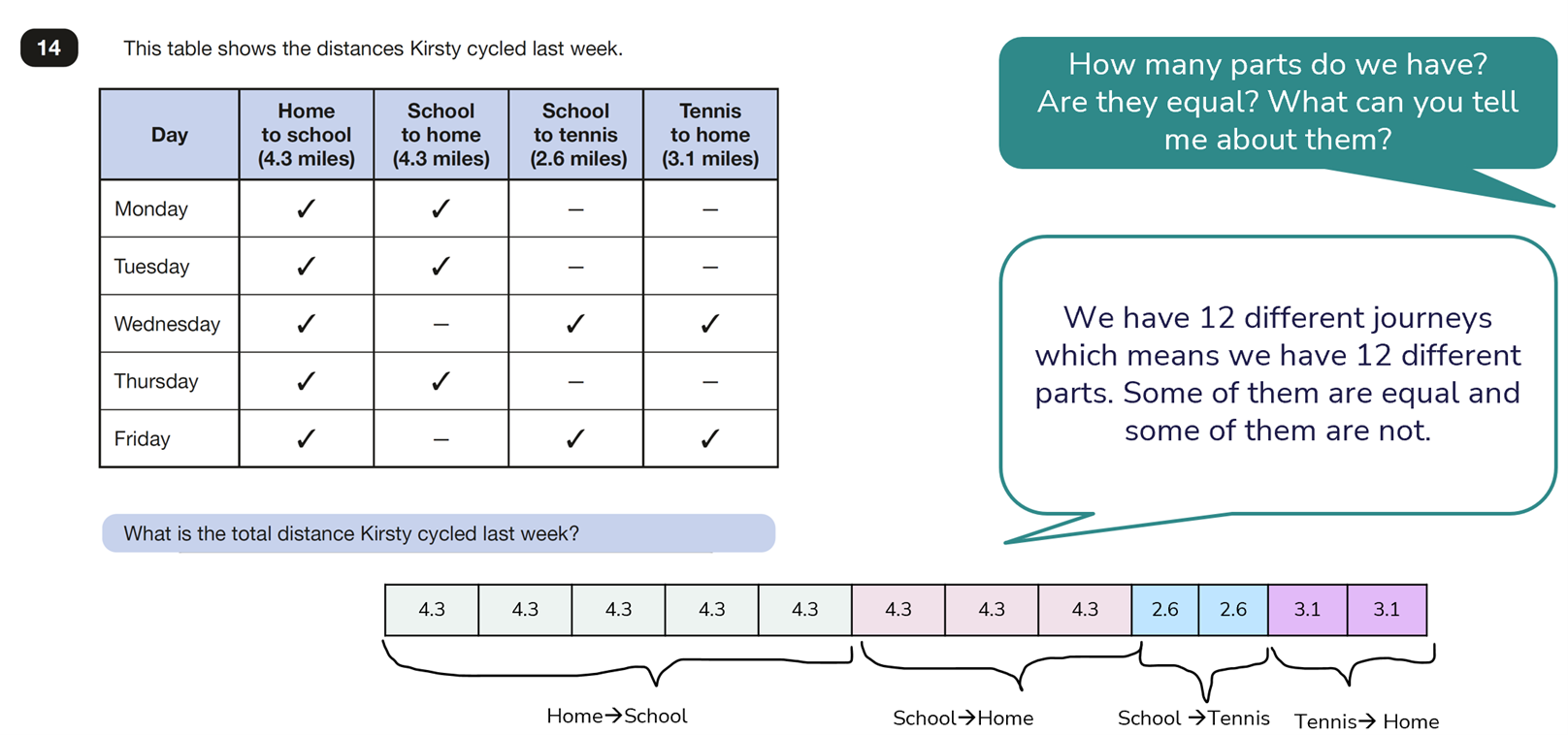
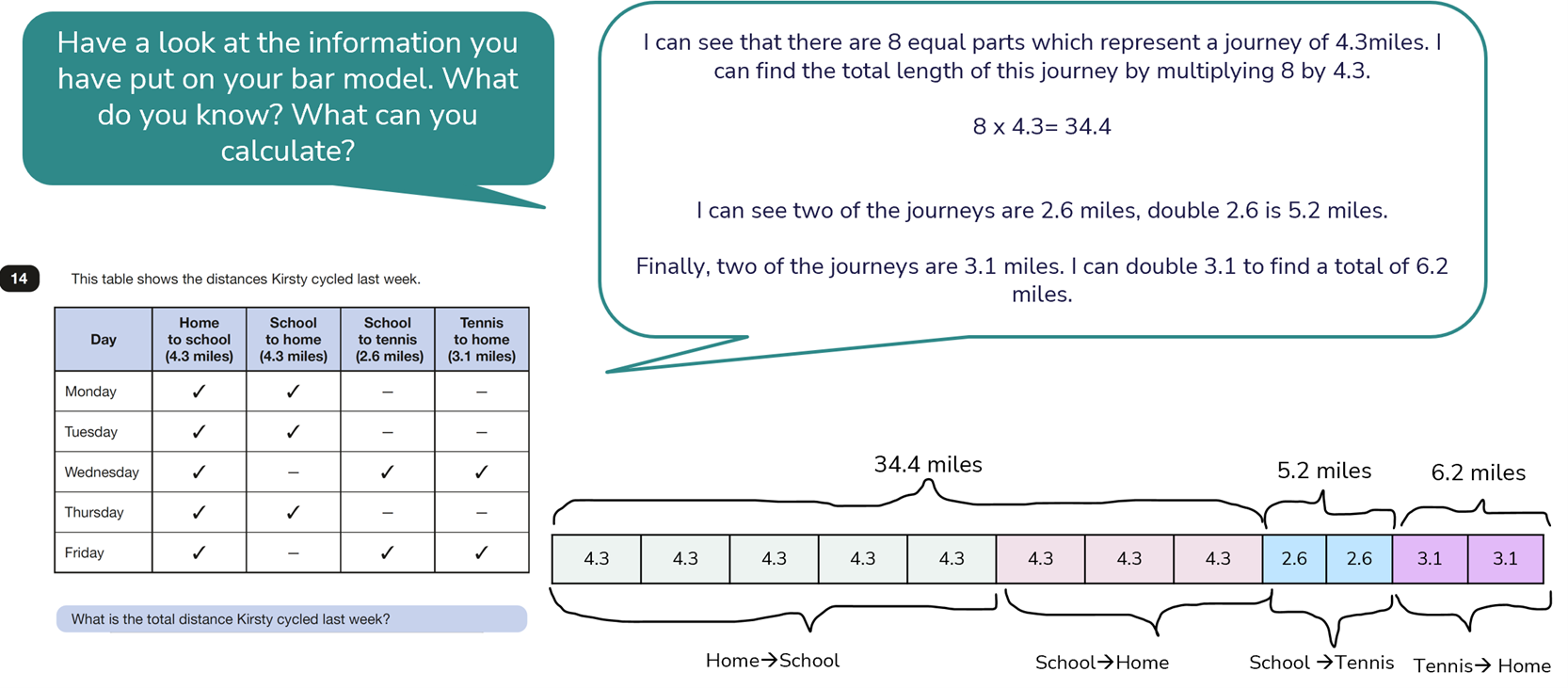
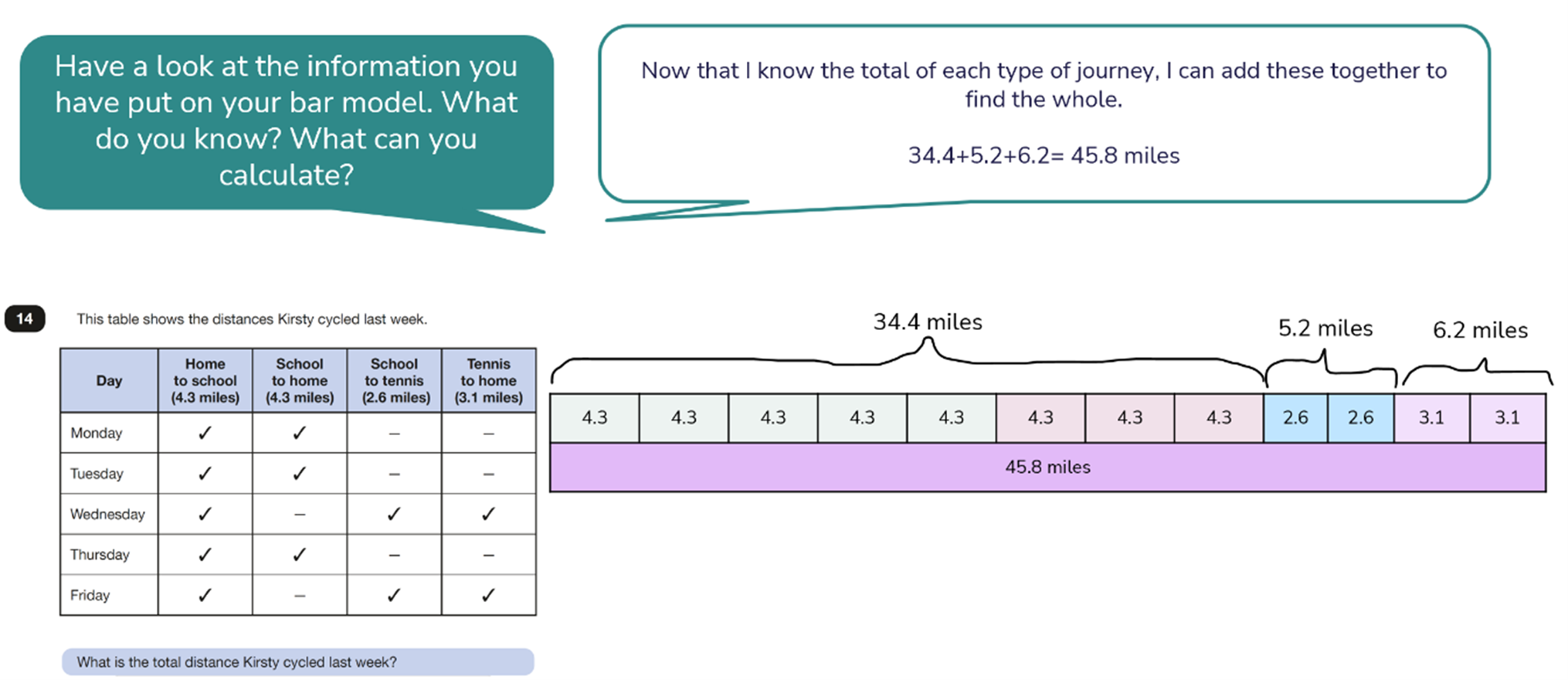
Solution:
The total number of miles cycled is 45.8 miles.
There are, of course, other ways to reach the same total amount, but these are also likely to involve addition and multiplication combined in some form. If children were to compare the bar models for different methods, they would see that the overall answer is still made by the same parts, just in another order.
Example 3:
2025 KS2 SATs – Mathematics Paper 2, question 19
Bar modelling to expose the need for division, addition and subtraction
In this third example the bar model is particularly helpful in supporting us to see that we are finding a part of the whole and then splitting that part up further. This can be challenging for children to visualise, and the bar model again exposes the necessary calculations to find the solution.

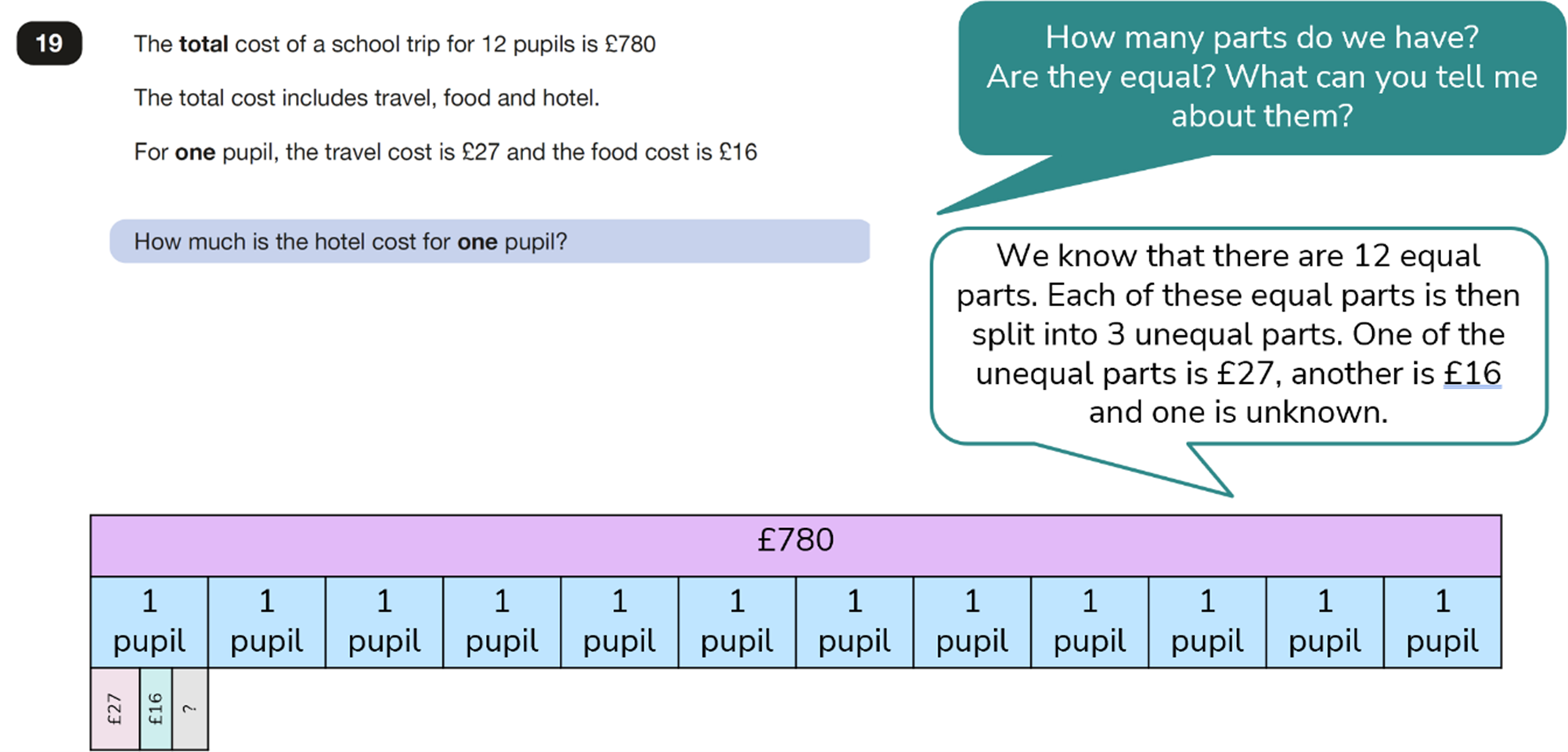

Solution:
The cost of the hotel for one pupil is £22.
By using a bar model to present what is known at each part of the question, we provide pupils with a way of breaking down the question into small steps. At each stage, new information can be added. In the first instance, the bar model supports us in uncovering the need to divide and in the second instance to use addition and subtraction.
Example 4:
2025 KS2 SATs – Mathematics Paper 2, question 23
Bar modelling to expose the need for multiplication and division
Questions involving proportion can often be tricky for children. However, if you look closely, we already have the beginnings of a bar model!
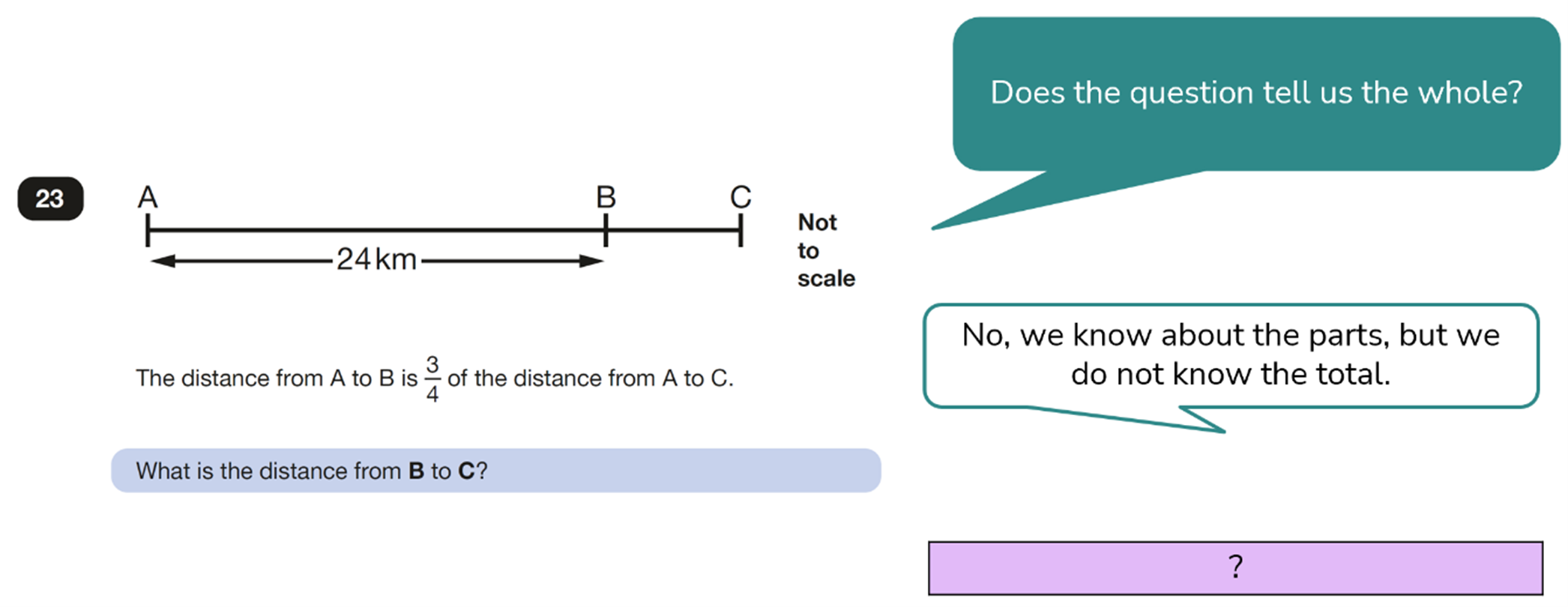
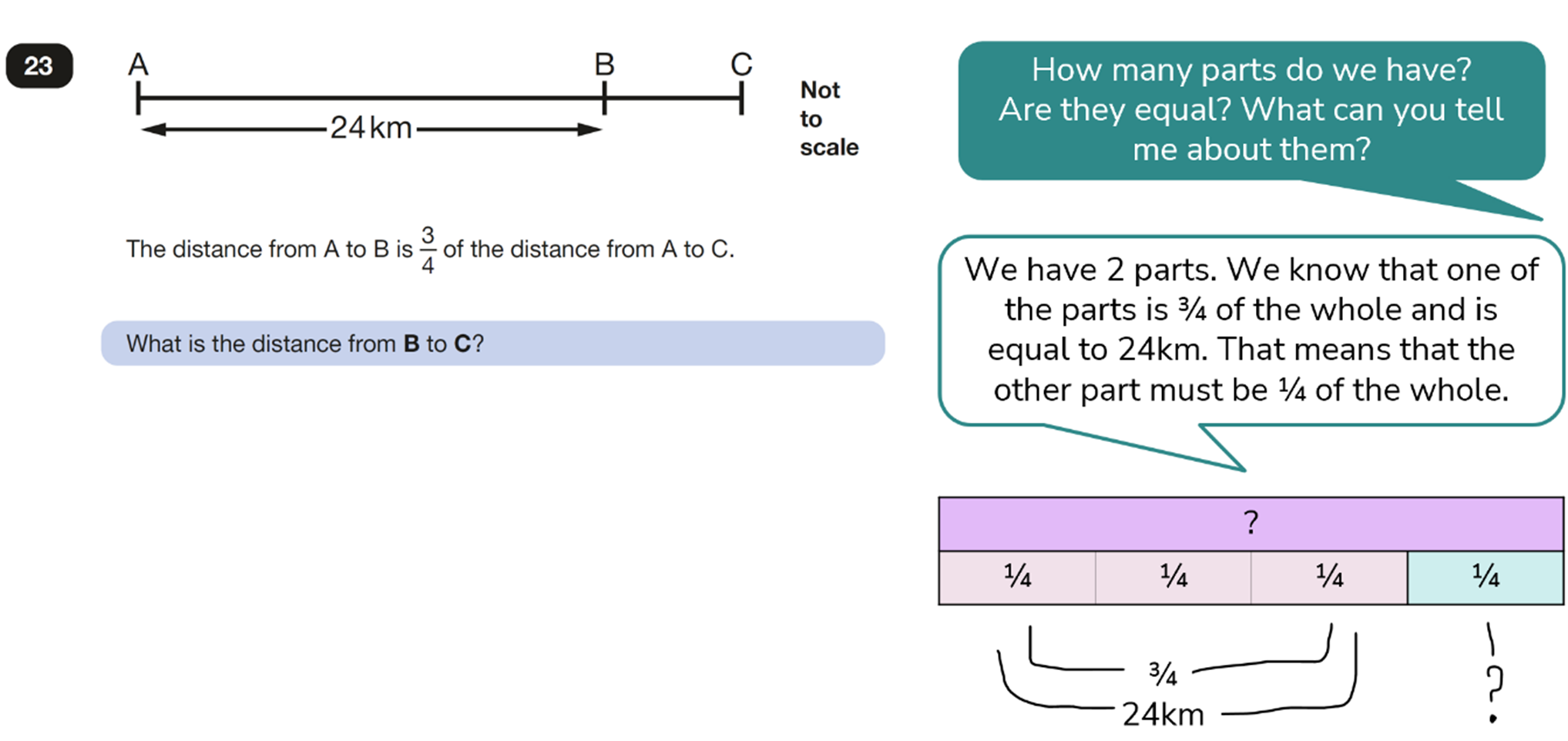
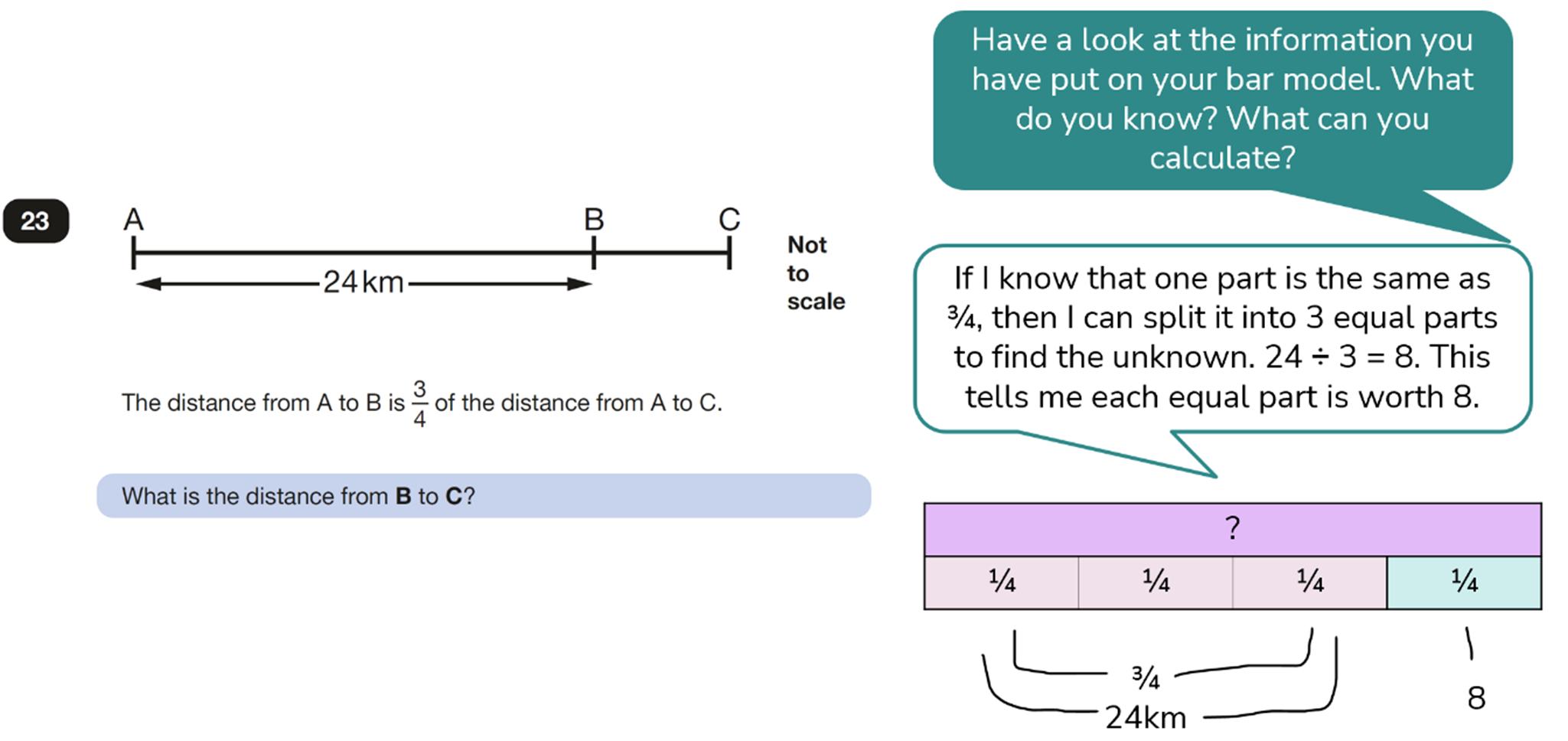
Solution:
The distance from B to C is 8km.
When children become familiar with the bar model and other similar models in mathematics, it enables them to make use of diagrams that are provided to them as part of a problem like in the question above.
Bar modelling isn’t just a strategy that is useful for children in year 6. The use of basic part whole models is something that can be introduced from the early years and used as a familiar model which can be built on with new learning. In this blog we have explored using the bar model to expose all four operations alongside the context of measures.
Laura Dell explores using the bar model for comparison when she takes a look at the KS2 SATs Paper 3 in the next instalment.
Further professional development
Our popular training is back this year in a new format.
Resources available on PA Plus which support with Bar Modelling and Year 6
Bar modelling in maths progression
- Download sample pages
- A combination of photos of concrete resources, pictorial bar models and abstract calculations brought together to exemplify how to solve problems from across the maths curriculum.
Year 6 maths gap finder: SATS preparation toolkit
- Diagnostic summative assessment papers for early identification of gaps.
- Resources to support teaching and rehearsal of arithmetic and reasoning.
- A suite of resources and analysis tools to identify specific areas of strength and development points for pupils and classes when using any past SATs papers as practice (2016-2024)






