This blog continues our series exploring how to enable children to showcase their mathematical understanding, reasoning and problem solving in the KS2 maths SATs papers. We know that for the reasoning papers, pupils need to be able to process and manage quite a range of information for some questions, and there needs to be specific teaching of strategies to enable them to do this.
In part 1 (Measures made visual: using bar modelling to support reasoning in KS2 SATs), the bar model was used to exemplify how to solve questions from reasoning paper 2 from the KS2 SATs 2025 with a particular focus on problems involving measures. And like our blog series from 2024, the focus of part and whole remains at the forefront.
In this blog, I will explore questions from the KS2 SATs Reasoning Paper 3. Like part 1, the focus will be on questions involving measures, as there were a number of these, in different styles and formats. Like part 1, there will also be a focus on part and whole. But in this blog, I will exemplify questions where bar modelling might not be an obvious strategy choice.
When you read the examples in this blog, you may find yourself thinking that bar modelling is not a particularly efficient strategy for the questions that I have chosen. I challenge you though to disregard efficient strategies for the time being and instead consider how exploring these questions in a visual way may aid the conceptual understanding which underpins the more efficient strategies your children will be aiming for.
Example 1:
2025 KS2 SATs – Mathematics Paper 2, question 10
Bar modelling focussing on proportion and comparison
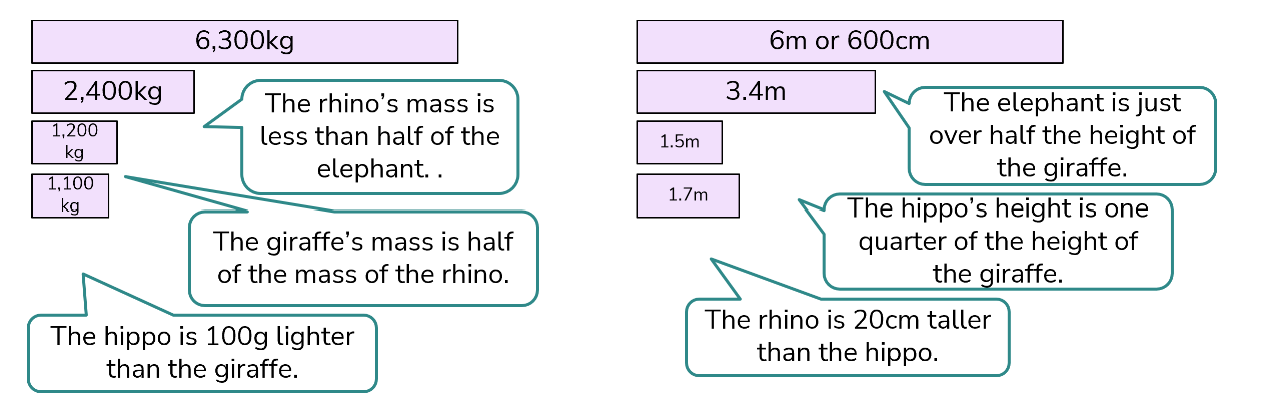
In this question, information is shared in a data table format. The table is followed by four statements, and we need to ascertain which are true and which are false.
For the first 3 statements, I have exemplified below how different multiplicative models can be useful to support children to uncover the needed calculations.
For the first statement, a comparison, or ratio model (as all parts are equal) is a useful visual aid.


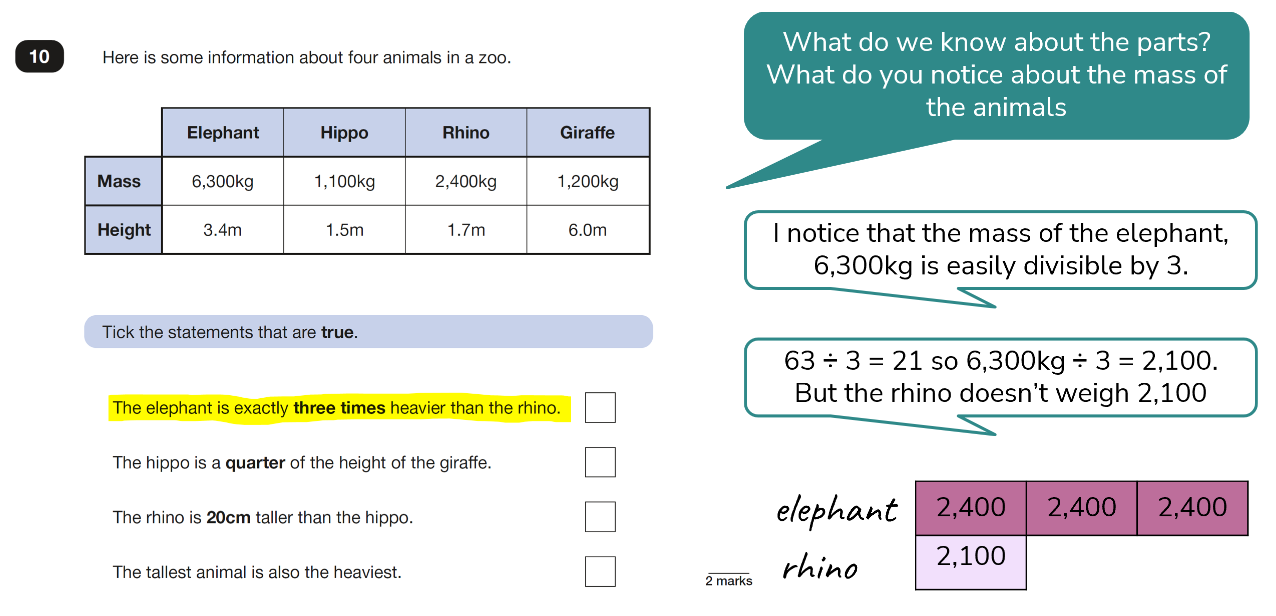
Solution (to this statement)
The first statement is false as the elephant would need to have a mass of 7,200kg.
The comparison, or ratio model, is useful here to illustrate the relationships between numbers and equal parts where multiplicative language such as ‘three times’ is used. In this case, we could either divide the greater mass by 3 or multiply the smaller mass by 3.
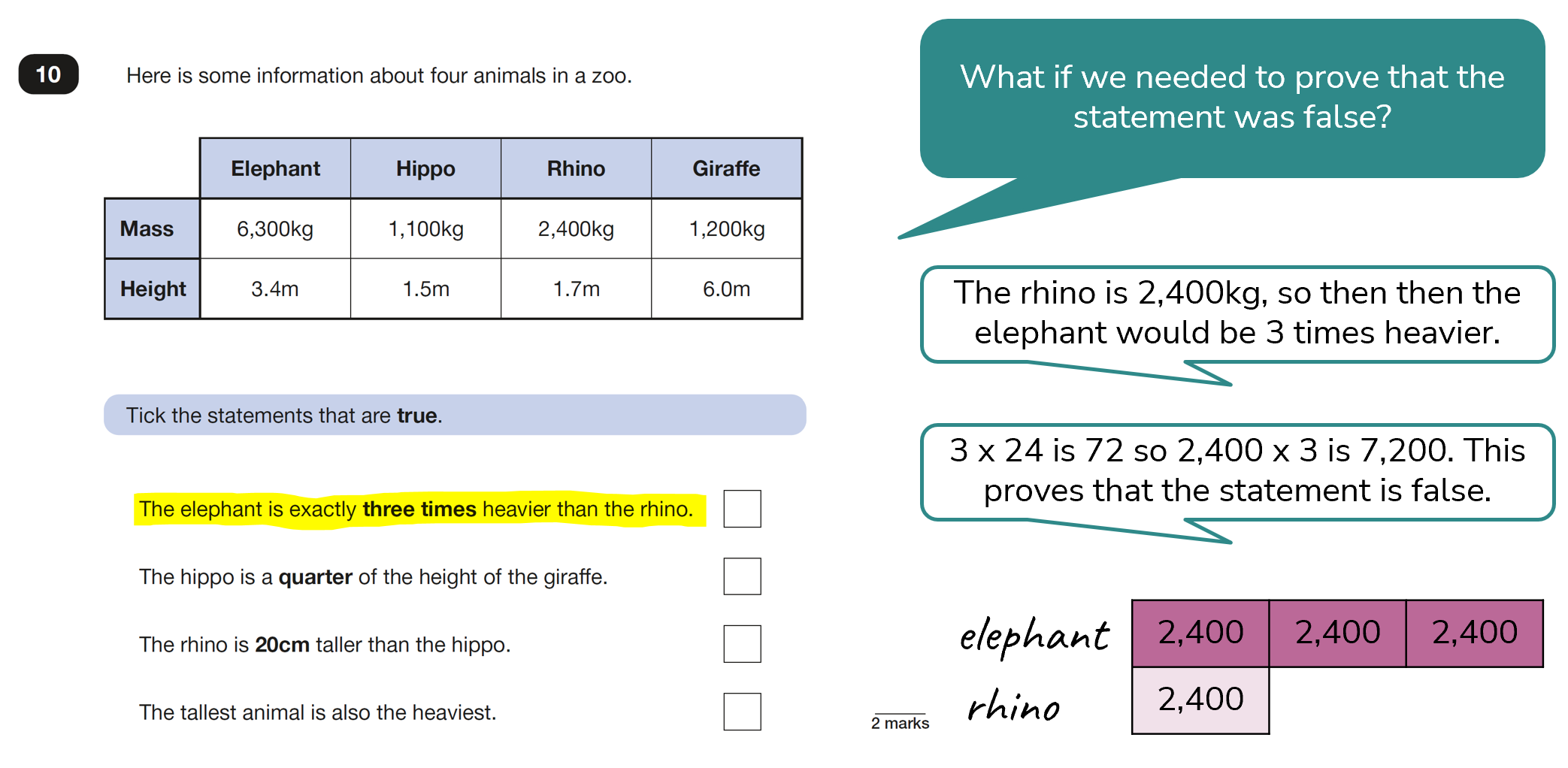
Now for statement 2.


Solution (to this statement)
The second statement is true as the hippo’s height is 1.5m which is one quarter of 6m.
Exploration of this statement using the bar model may be a useful reminder of models used to find fractions of amounts where all of the parts are equal and the whole is the total of the equal parts. In this example, I have used division to find the answer, but I could also have used multiplication and multiplied the hippo’s height by 4 to see if this matched the given height of the giraffe.
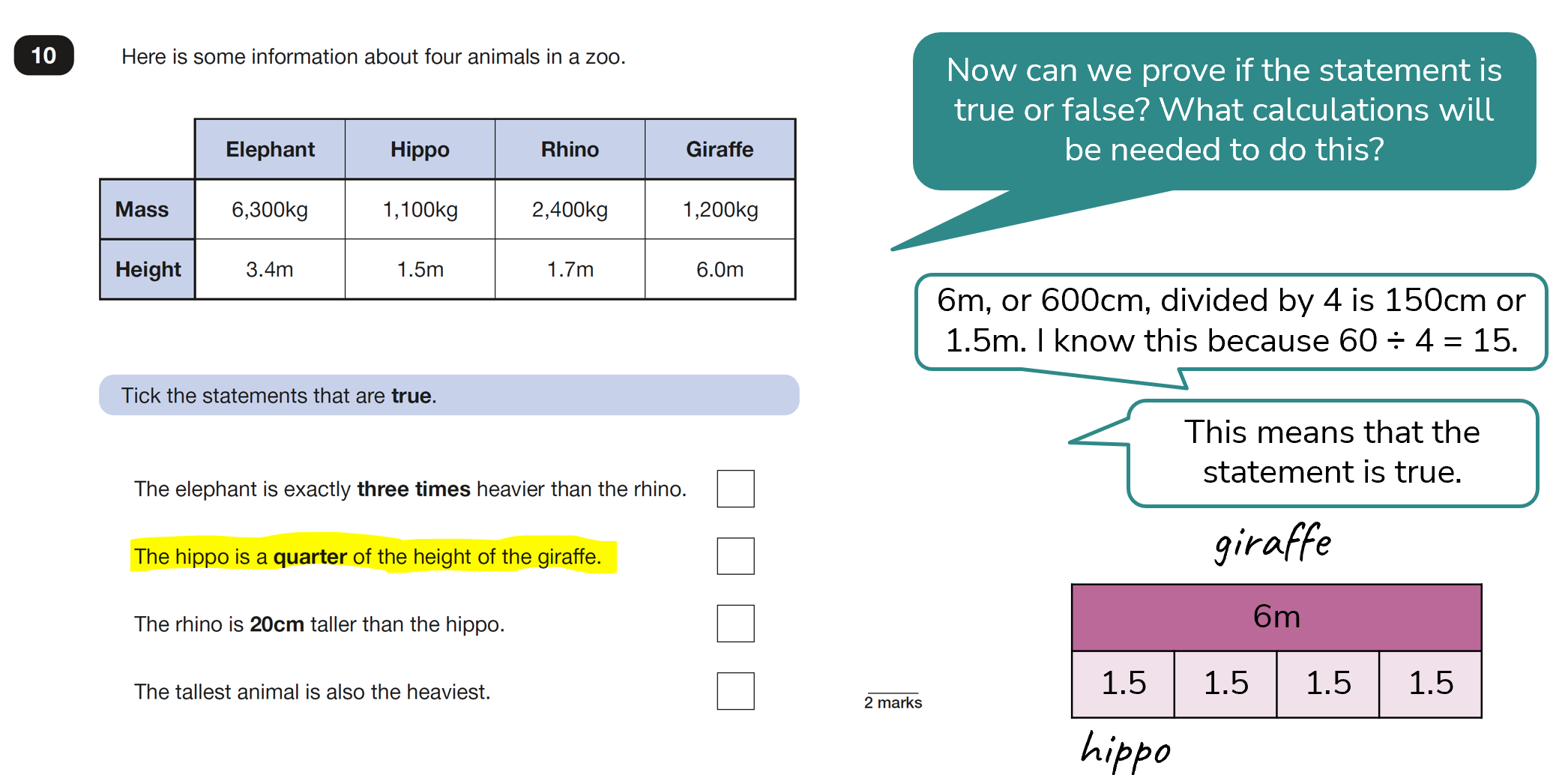
For statement 3, a multiplicative model (involving equal parts) would not be helpful as this statement is asking us to consider the difference.



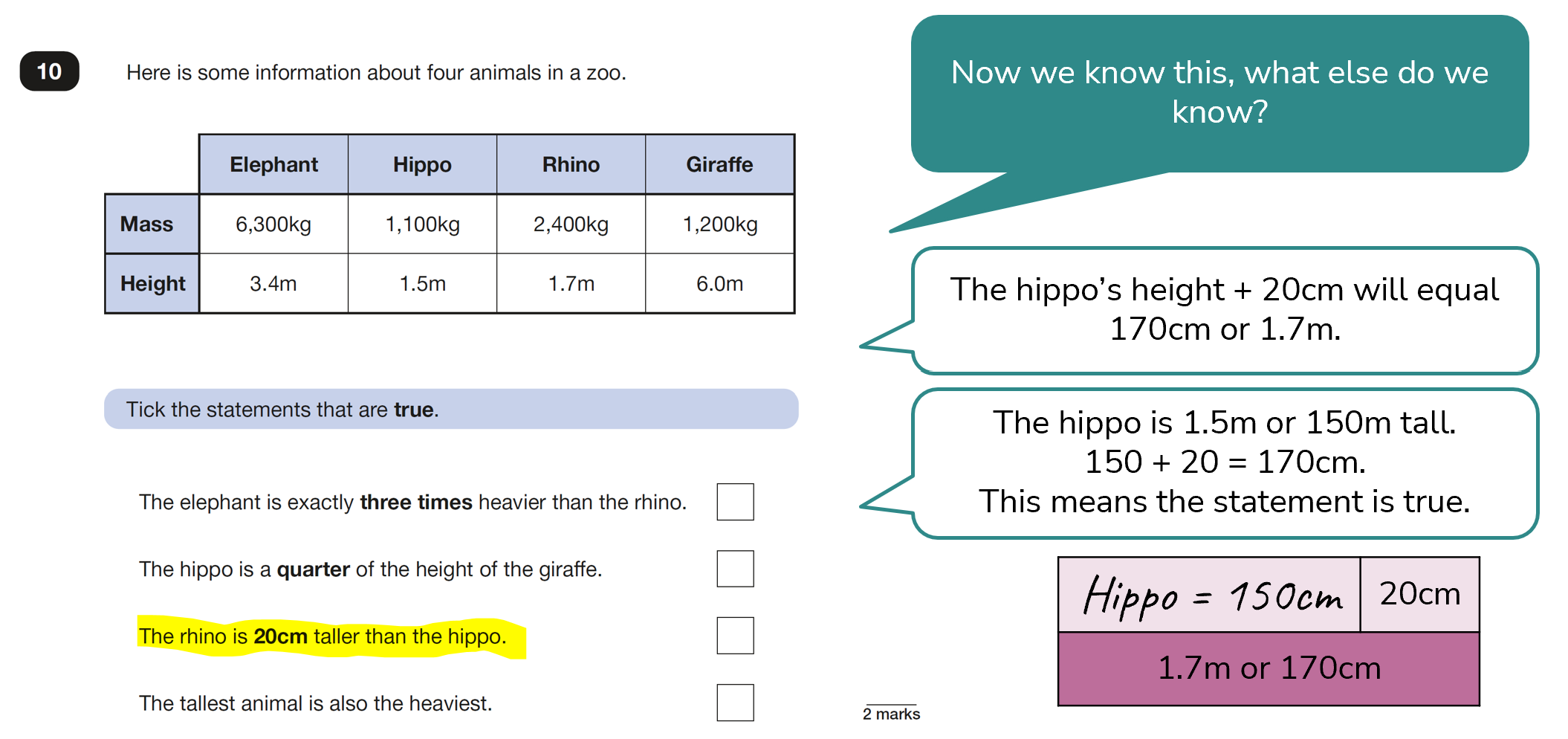
Solution (to this statement)
The third statement is true as the rhino’s height (1.7m) is 20cm greater than the hippo’s (1.5m).
I know that models involving the difference, and/or language such as ‘taller than’ can be tricky to visualise and so the bar model, where the whole can be compared with the parts, is a useful way of reinforcing this.
Although not exemplified here, the final statement could be used to consider proportional relationships in both the heights and the masses of the animals when constructing bar models and considering how accurately we can draw them.
Solution to the question
Statements two and three are true.
Example 2:
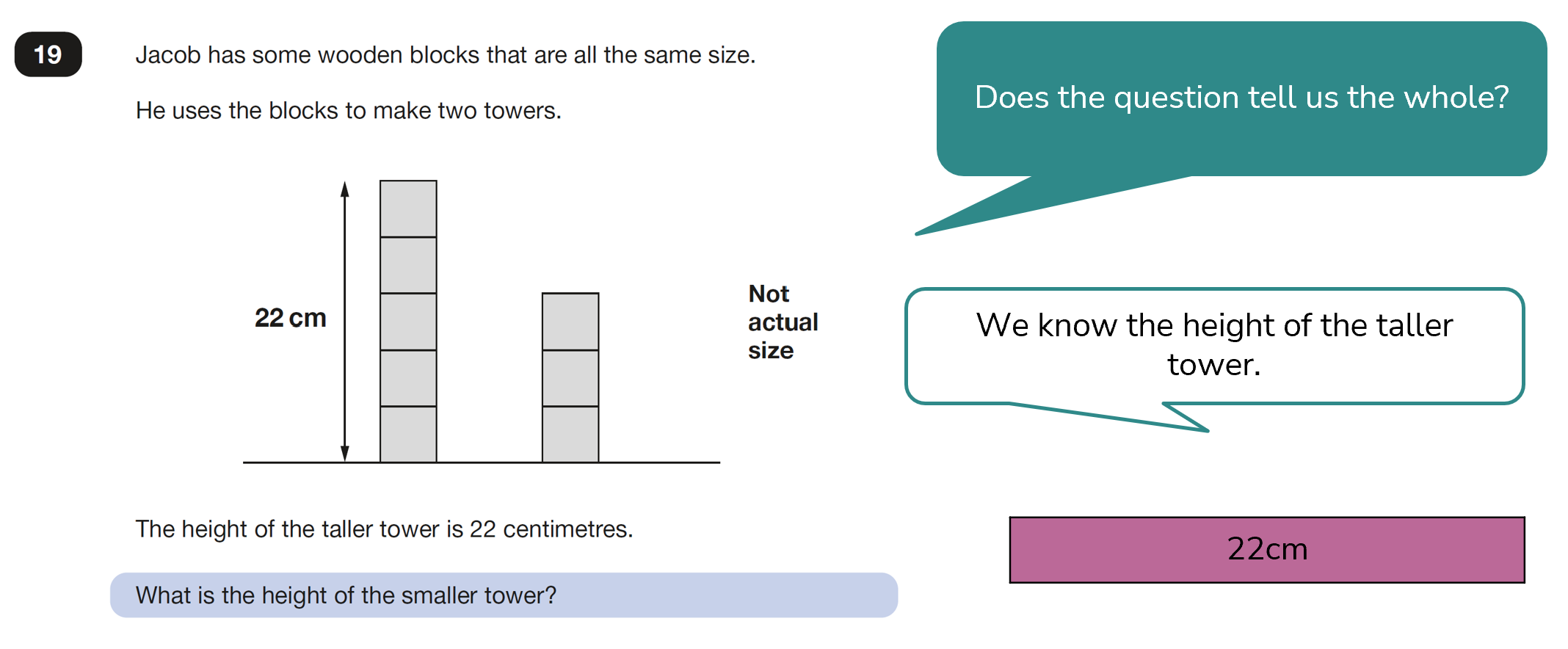
2025 KS2 SATs – Mathematics Paper 3, question 19
Bar modelling focussing on equal parts
The information in this question is almost already presented to us as a bar model but perhaps in a less familiar, vertical representation. By putting the information into horizontal bars, and once again using a comparison, or ratio model (as all the parts, or blocks in this case, are equal), the operations needed to solve the problem become much clearer.
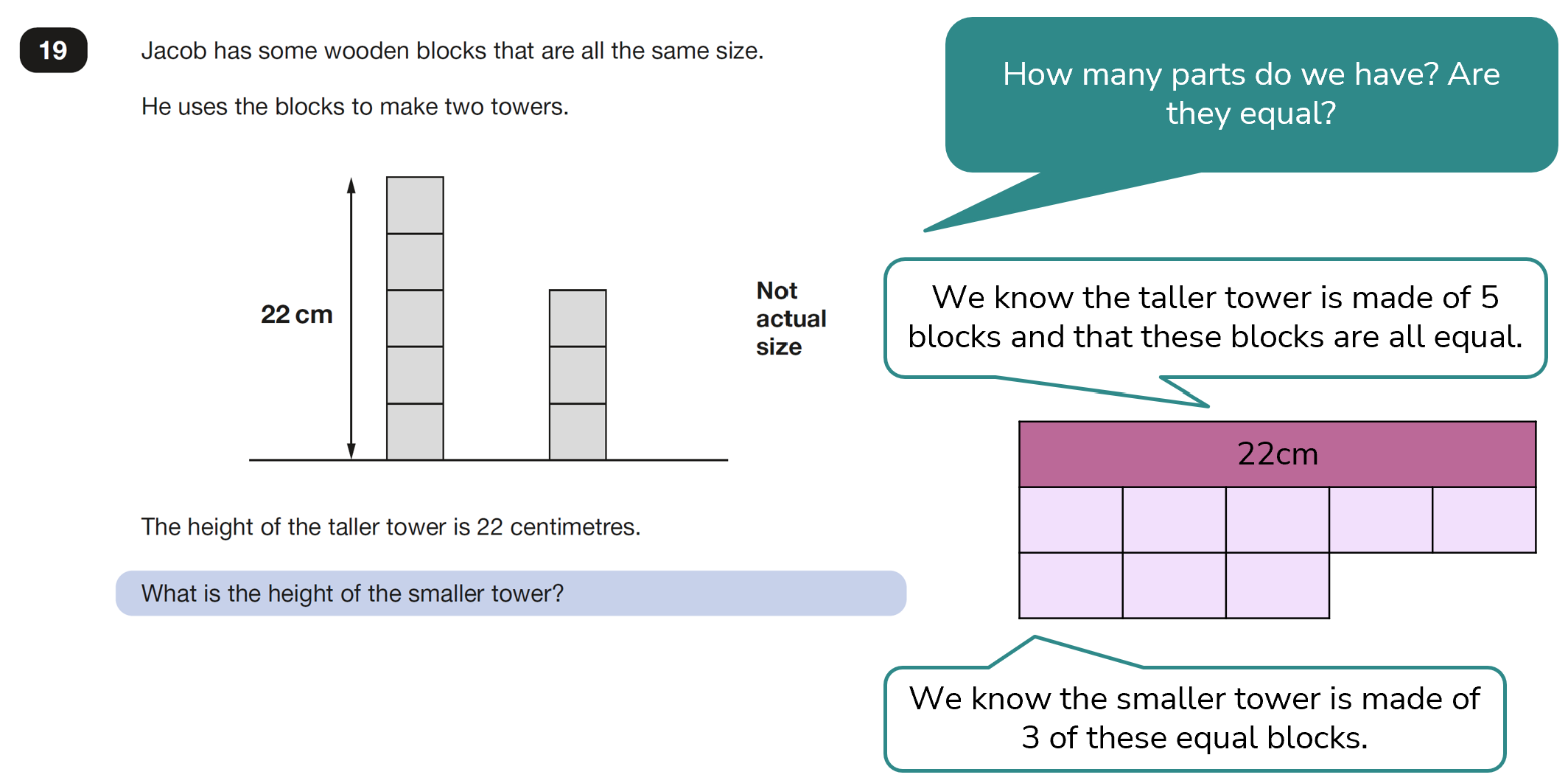
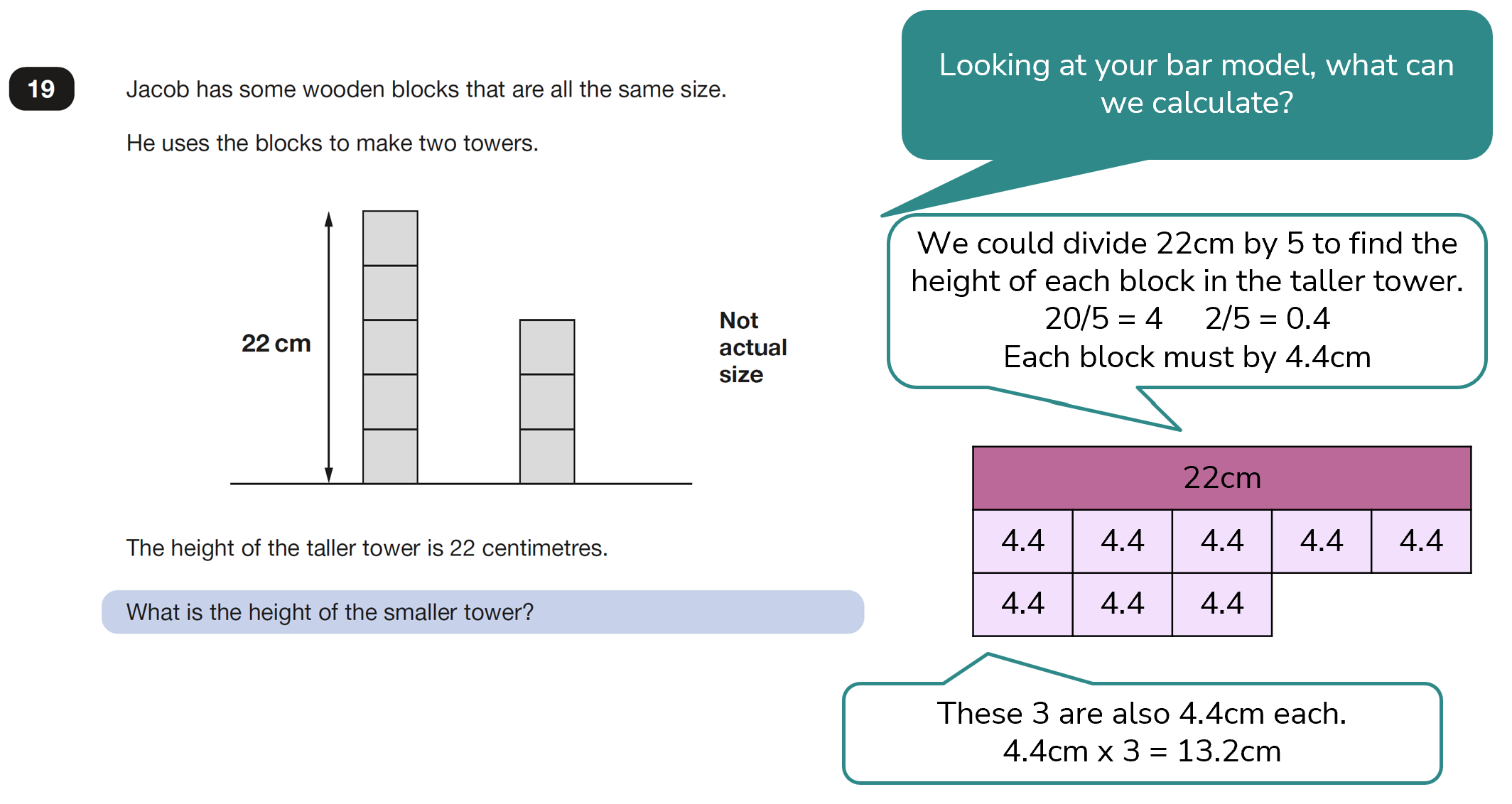
Solution
The height of the smaller tower is 13.2cm.
As well as the bar model being a useful tool for this question, this question is also helpful in highlighting the importance of base facts. Here, as long as we know that 20 divided by 5 equals 4, then we can use this fact to help us to calculate that 2 divided by 5 will be 0.4. We can draw on the relationship that 2 is ten times smaller than 20 so the quotient of 2 divide by 5 will be ten times smaller than the quotient of 20 divided by 5.
Example 2:
2025 KS2 SATs – Mathematics Paper 3, question 22
Bar modelling focussing on part and whole in the contexts of missing angles
Bar modelling might not be an obvious tool for this question but once we pull on our knowledge of interior angles in shapes and on a straight line, the usefulness of considering parts and wholes becomes clearer and helps to make a complex question much simpler.
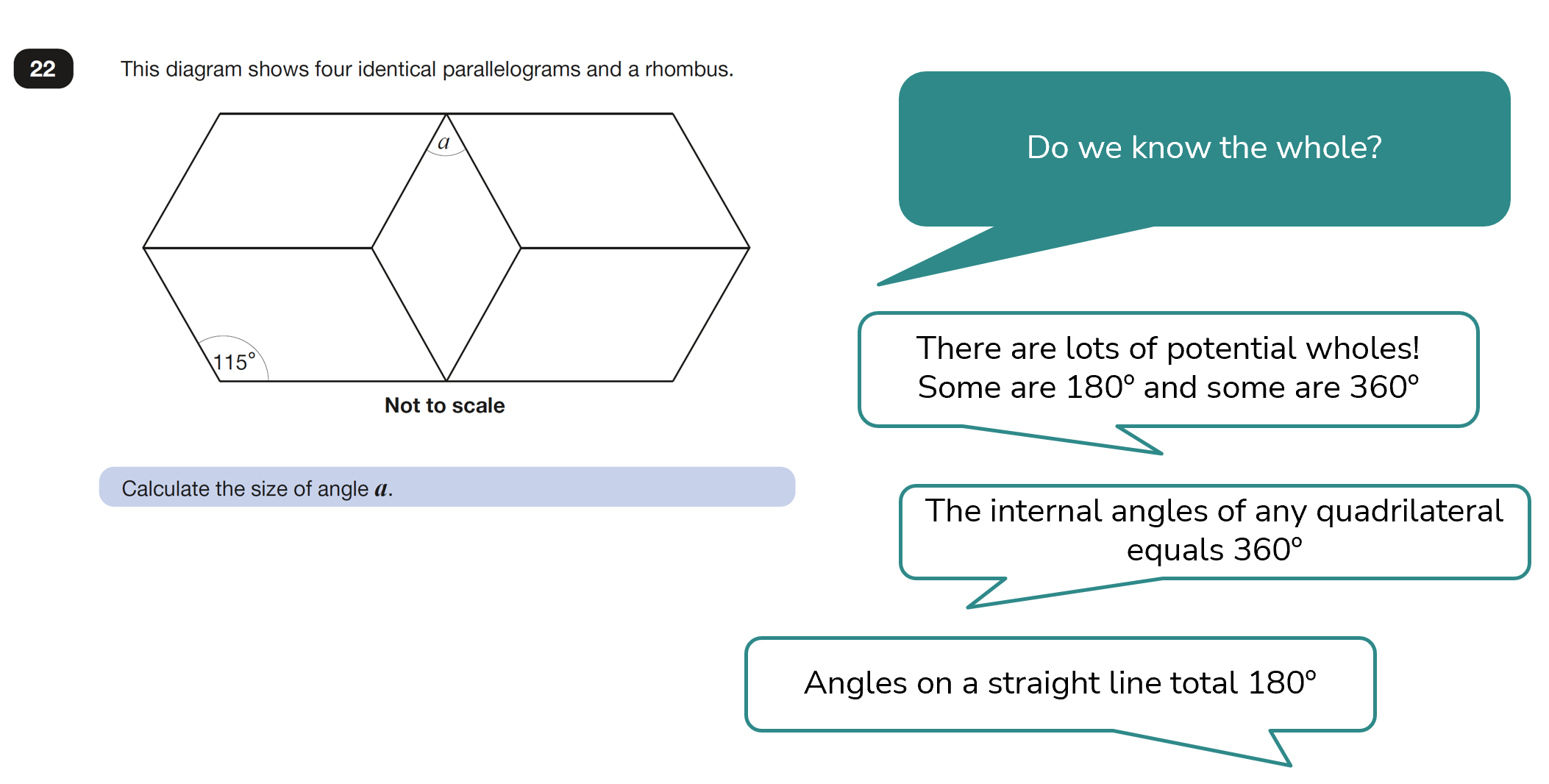
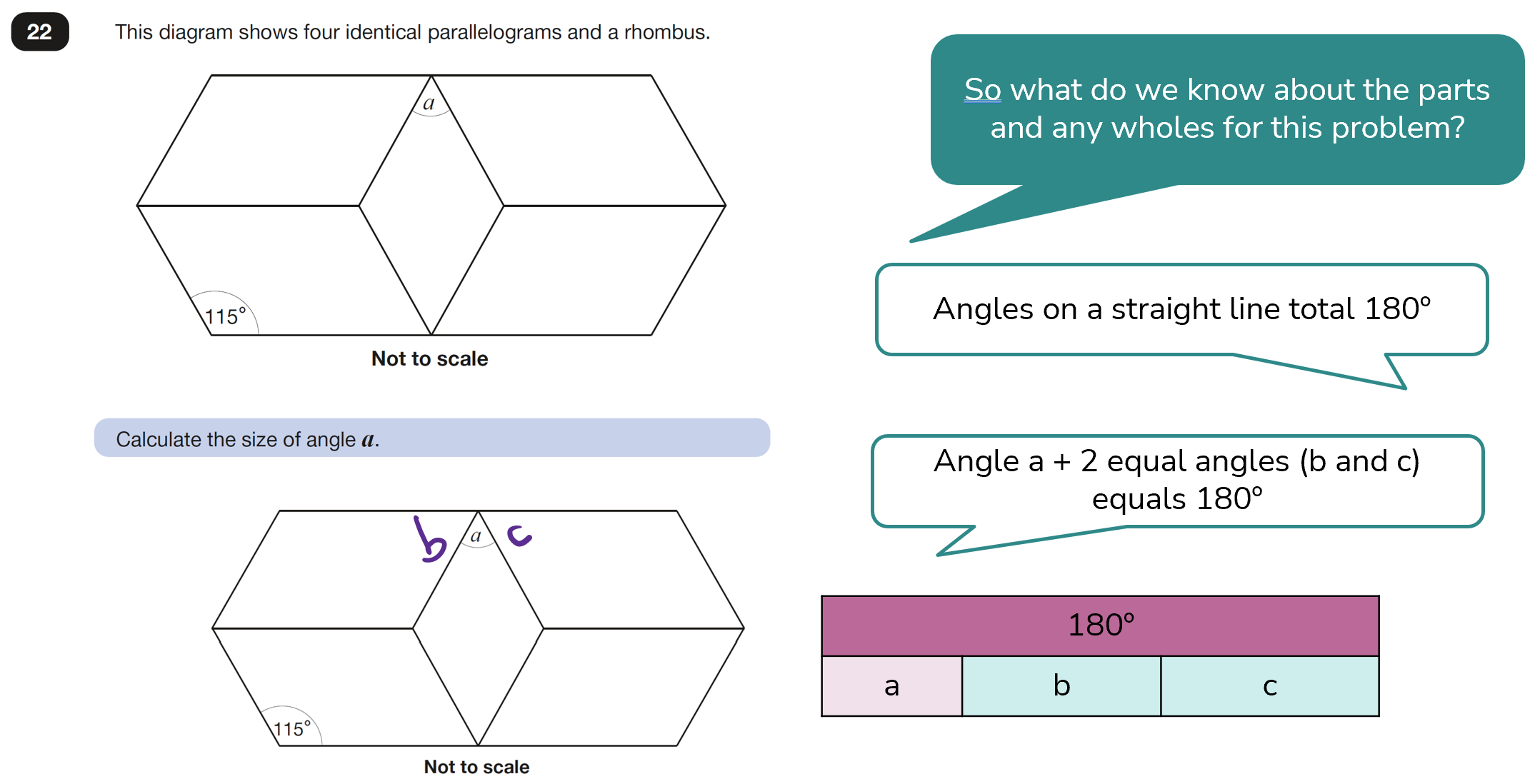
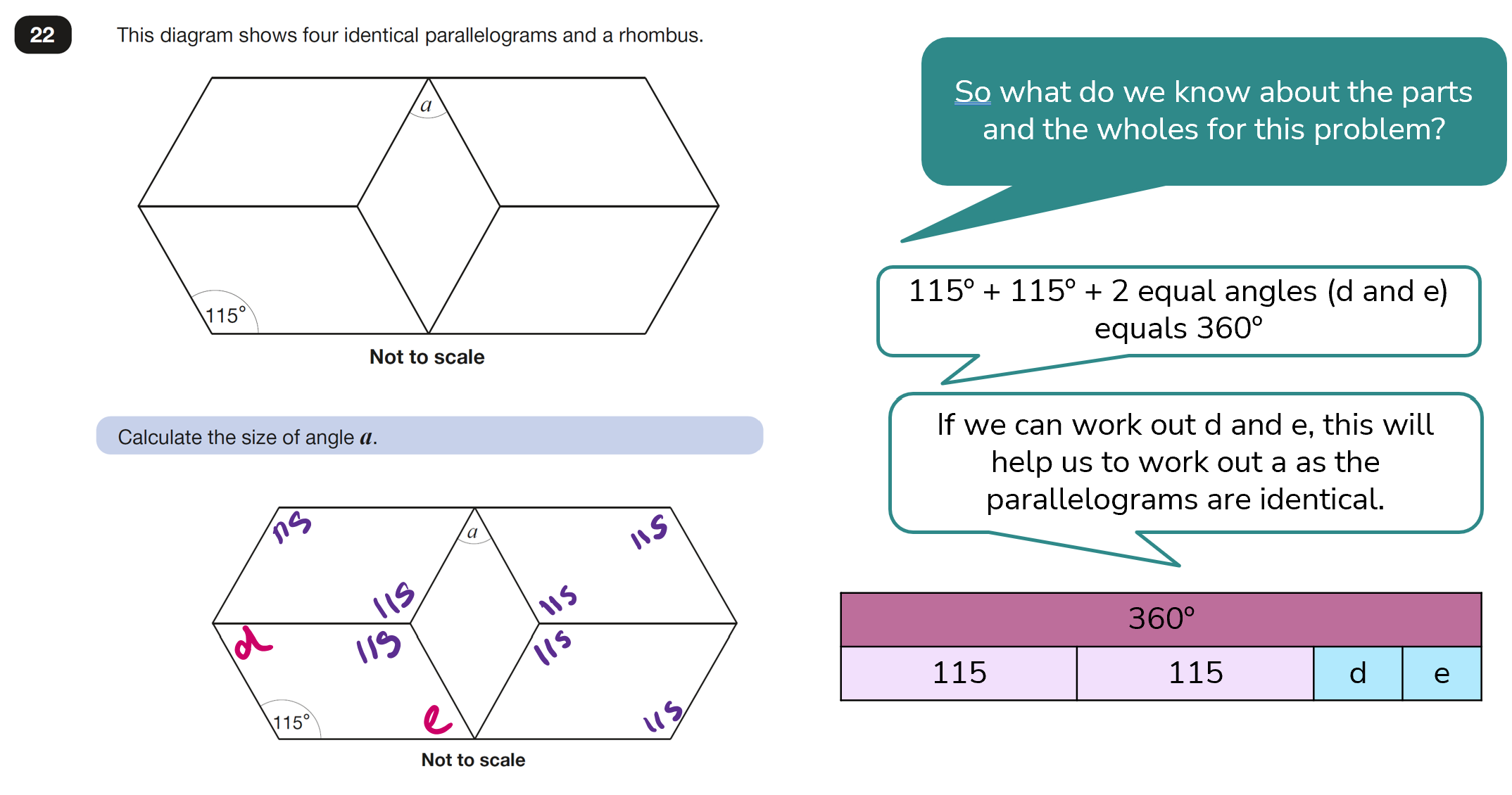
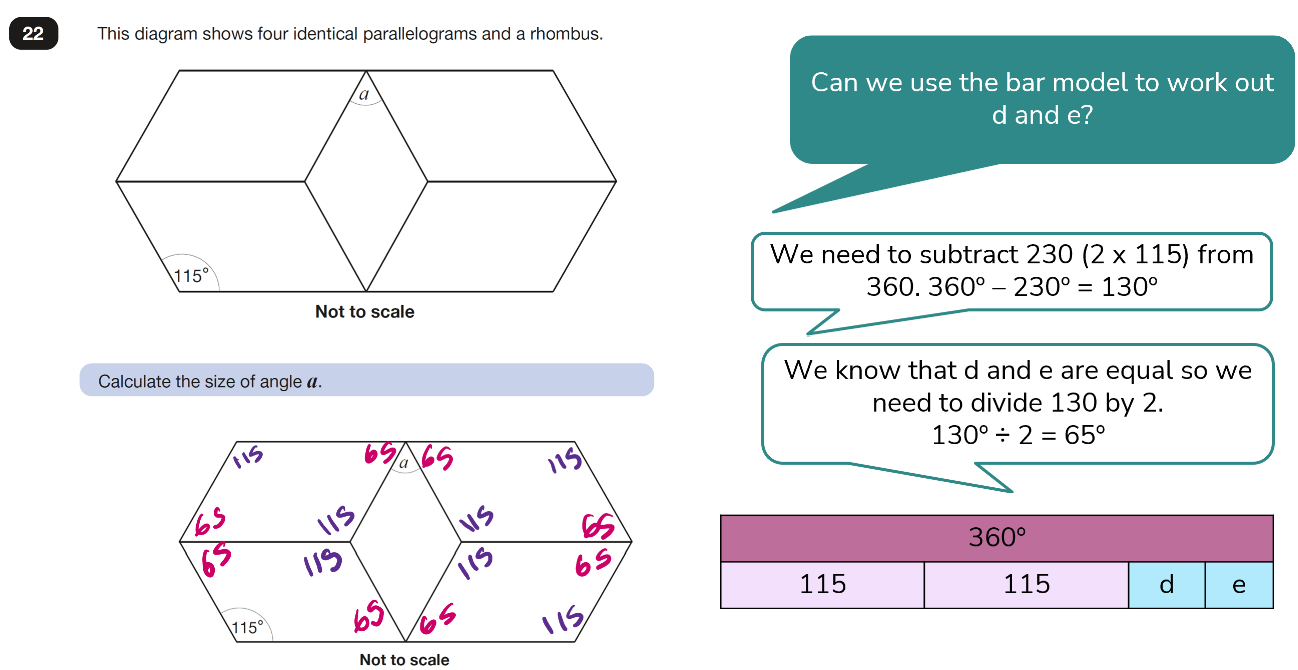
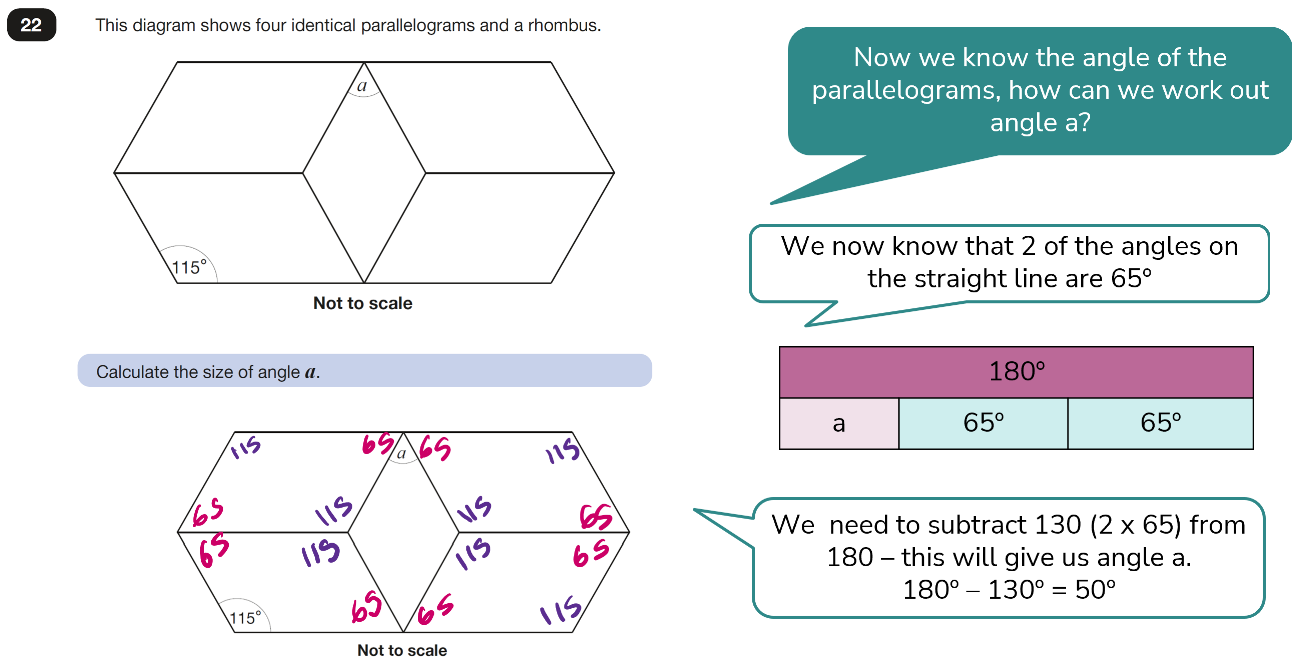
Angle a equals 50°.
By using different bar models to present what is known about each of the shapes including angle a and then angle b, this helps us to consider each whole in turn and gives us a good starting point in solving the problem.
As Charley states at the end of blog 1 in this year’s SATs bar modelling series, bar modelling isn’t just a useful strategy for solving these questions at the end of KS2 – Year 6 – but a strategy that could be taught, rehearsed and honed as children move through the primary phase. In addition, bar modelling is a thoroughly useful tool for assessment for learning as through building and exploring models, possible misconceptions are often uncovered. Hopefully, no matter what year group you teach in, by exploring these KS2 assessment examples, you can link these to your year group curriculum whether that be exploring part and whole in addition and subtraction in KS1 to moving into more complex multiplicative models in KS2
Further professional development
Our popular training is back this year in a new format.
Across four half-day sessions, we unpick tools for supporting children in meeting age-related expectations in maths using a range of different strategies, including the bar model!
Resources available on PA Plus, all included within the subscription and some also available as a separate purchase if you are not subscribed, which support with Bar Modelling and Year 6:
Bar modelling in maths progression
- Download sample pages
- A combination of photos of concrete resources, pictorial bar models and abstract calculations brought together to exemplify how to solve problems from across the maths curriculum.
Year 6 maths gap finder: SATS preparation toolkit
- Diagnostic summative assessment papers for early identification of gaps
- Resources to support teaching and rehearsal of arithmetic and reasoning
- a suite of resources and analysis tools to identify specific areas of learning strength and development for pupils and classes when using any past SATs papers as practice (2016-2024).



