
What makes good teaching?
I have been thinking hard about pedagogy and recently revisited Rosenshine’s Principles of Instruction. He draws on multiple sources to try to identify what makes good teaching. He identifies ten instructional principles and summarises what most effective teachers do.
He says:
“The most effective teachers ensured that their students efficiently acquired, rehearsed, and connected background knowledge by providing a good deal of instructional support. They provided this support by teaching new material in manageable amounts; modelling, guiding student practice, helping students when they made errors and providing sufficient practice and review.” (₁)
Simple right? Wrong!
Teaching is a complex process
We all know that teaching is a complex process; not only do we need to consider the learning point we are trying to teach, but we also have 30 ‘variables’ in the classroom that all come with their own learning needs, knowledge, and experience. We need to think carefully about how we are going to deliver the learning and provide appropriate rehearsal. In this blog, I want to focus on one aspect: modelling. More precisely, initial models that support and scaffold thinking – where our thinking can be exposed.
Carefully planned modelling to make the implicit explicit – talking out loud
Tom Sherrington (₂) talks about the importance of teachers modelling their own thought processes and says that this supports students in developing their capacity for metacognition and self-regulation.
He states that effective teachers are able to able to narrate the decisions and choices they make by making the implicit explicit. In the EEF guidance report on metacognition and self-regulated learning (₃), it says that teachers very rarely plan this explicit modelling as it comes ‘naturally’ but when not planned, it risks keeping many things implicit. For pupils (novices) to become experts, they need to know how the expert (the teacher) thinks and acts. The implicit needs to be made explicit.
Modelling – bridging the gap between the teacher model, guided practice and independent rehearsal
I want to share some simple ways to use practical resources with jottings and / or speaking frames to help plan for explicit modelling of thinking. I believe that these can bridge the gap between teacher modelling, guided practice, and independent rehearsal. Therefore, they help to secure learning.
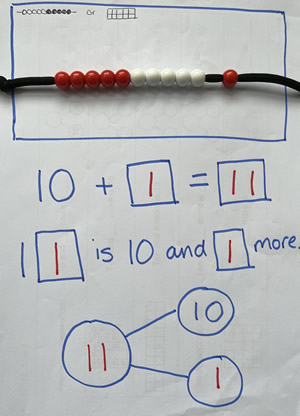
This example supports understanding of ‘ten and some more’; understanding how the unit of ten is created. It exposes the fact that the numbers 11-19 are a ten and some ones. This simple frame makes the link between the practical resource (in this case, a beadstring), the calculation, the language and the part, whole model.
All show eleven as ten and one more. Whilst articulating my thoughts, I would make explicit the links between different representations; specifically, the fact they are all representing the same value – eleven – in different ways.
The use of language needs to be carefully considered and connections between symbols / models and the language made explicit. For example, the + symbol in the calculation, the ‘and’ in ‘10 and 1 more’ and the lines that link the parts to the whole in the part, whole cherry model all represent that 10 and 1 are combined to make 11.
Modelling how to find fractions of amounts
In this video, finding fractions of amounts is modelled. A drawn model is used alongside the speaking frame.
In this video, the same learning – calculating fractions of amounts - is modelled using double-sided counters and jottings to track the solving of the problem.
Articulation of what is known and unknown (and therefore what needs to be found out) features in both examples.
Modelling how to find the difference between amounts
In this example, calculating the difference between amounts is the focus of the learning using money as the context.

The part, whole bar model makes explicit the fact that the difference is the missing part when comparing the whole and the known part.
The speaking frame supports the calculation of the difference as finding ‘how many more’ - counting on from the known part (30p) to the whole (60p).
It then links this to difference and then the subtraction calculation.
After practice, so understanding of difference is secure, the link between finding the difference and finding change using money can be made.
Connecting finding the difference and calculating change
For example, if some toy cars costing £8 are paid for with a £20 note, what would the change be?


This can be put into an initial sentence to make what is known and unknown explicit.
I know the cost - £8; I know the amount paid - £20.
The part, whole bar model helps us to identify what is unknown – the change or difference.
The link between the model and the calculation should be familiar from the previous practice so the change can be found and the problem solved.
Do children understand the concept or are they simply completing a task?
The element we have looked at in the blog may last only a couple of minutes within your lesson, but the initial explicit model is essential to enable pupils to understand the learning and not just complete the task. Time during planning is needed to ensure that the initial model used enables you as the teacher to articulate your thinking as the expert.
Five things to remember when planning the modelling in maths:
To effectively plan the initial explicit model and articulation of your thinking:
1. Be clear about what the focus of the learning is and ensure the learning is front and centre in the model – not the task.
2. Link practical resources, language, models and calculations and make the connections between them explicit within your articulated thinking.
3. Make the initial scaffold that is used within explicit teaching reusable so it can be used within guided and independent practice.
4. Have the scaffold written on a large scale that can be seen by all children. It can go on your working wall and can be referred to regularly.
5. Take time to plan what you are going to say; write a script if it helps. This will ensure that you model using precise and accurate mathematical vocabulary.
Feeling inspired?
Join the HFL Education Primary Maths Team for up coming training and events.
To keep up to date: Join our Primary Subject Leaders’ mailing list
To subscribe to our blogs: Get our blogs straight to your inbox
References
1. Rosenshine, B. (2012) Principles of instruction, Research based strategies that all teachers should know. American Educator
2. Sherrington, T (2019) Rosenshine’s principles in action. John Catt Educational Ltd. @teacherhead
3. EEF guidance report: Metacognition and self-regulated learning Metacognition and Self-regulated Learning | EEF (educationendowmentfoundation.org.uk)



